题目内容
已知函数![]() .
.
(Ⅰ)求函数![]() 的最大值及相应的自变量
的最大值及相应的自变量![]() 的集合;
的集合;
(Ⅱ)该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
解:(Ⅰ) ∵![]()
![]()
![]()
![]()
∴当![]() 时,函数
时,函数![]() 取最大值,最大值为
取最大值,最大值为![]() ,此时自变量
,此时自变量![]() 的取值为
的取值为![]() ,即
,即![]()
故函数![]() 的最大值为
的最大值为![]() ,自变量
,自变量![]() 的集合是
的集合是![]()
(Ⅱ)方法一:将函数![]() 的图象依次进行如下变换:
的图象依次进行如下变换:
()先把函数![]() 的图象上所有点向右平移
的图象上所有点向右平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象;
的图象;
()再把函数![]() 的图象上所有点的纵坐标不变,横坐标缩短为原来的
的图象上所有点的纵坐标不变,横坐标缩短为原来的![]() 倍,得到
倍,得到![]() 的图象;
的图象;
()最后把函数![]() 的图象向上平移
的图象向上平移![]() 个单位长度,就可得到
个单位长度,就可得到![]() 的图象.
的图象.
方法二:将函数![]() 的图象依次进行如下变换:
的图象依次进行如下变换:
()先把函数![]() 的图象上所有点的纵坐标不变,横坐标缩短为原来的
的图象上所有点的纵坐标不变,横坐标缩短为原来的![]() 倍,得到
倍,得到![]() 的图象;
的图象;
()再把函数![]() 的图象上所有点向右平移
的图象上所有点向右平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象;
的图象;
()最后把函数![]() 的图象向上平移
的图象向上平移![]() 个单位长度,就可得到
个单位长度,就可得到![]() 的图象.
的图象.

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.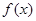 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求