Question

已知直线l经过A,B两点，且A(2,1)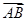， =(4,2).

(1)求直线l的方程；

(2)圆C的圆心在直线l上，并且与x轴相切于(2,0)点，求圆C的方程．

 

Answer 1

【答案】

（1）x-2y=0．（2）(x-2)²+(y-1)²=1． 

【解析】

试题分析：解：(1)∵A(2,1),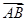 ="(4,2)"

∴B(6,3)

∵直线l经过A,B两点

∴直线l的斜率k=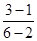=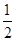，                       2分

∴直线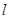的方程为y-1 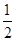(x-2)即x-2y=0．             4分

法二：∵A(2,1),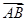 =(4,2)

∴B(6,3)                                         1分

∵直线l经过两点(2,1),(6,3)

∴直线的两点式方程为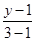=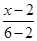，                    3分

即直线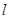的方程为x-2y=0．                           4分

(2)因为圆C的圆心在直线l上，可设圆心坐标为(2a,a)，

∵圆C与x轴相切于(2,0)点，所以圆心在直线x=2上，

∴a=1，                         6分

∴圆心坐标为(2,1)，半径为1，

∴圆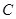的方程为(x-2)²+(y-1)²=1．              8分

考点：直线的方程，圆的方程

点评：解决的关键是根据两点式求解直线方程，以及圆心和半径求解圆的方程，属于基础题。