题目内容
15.已知命题p:方程$\frac{x^2}{t+1}+\frac{y^2}{3-t}=1$所表示的曲线为焦点在y轴上的椭圆;命题q:实数t满足不等式t2-(a-1)t-a<0.(1)若命题p为真,求实数t的取值范围;
(2)若命题p是命题q的充分不必要条件,求实数a的取值范围.
分析 (1)由方程$\frac{x^2}{t+1}+\frac{y^2}{3-t}=1$所表示的曲线为焦点在y轴上的椭圆,可得3-t>t+1>0,解出即可得出.
(2)由于命题P是命题q的充分不必要条件,可得-1<t<1是不等式t2-(a-1)t-a<0解集的真子集,解出即可得出.
解答 解:(1)∵方程$\frac{x^2}{t+1}+\frac{y^2}{3-t}=1$所表示的曲线为焦点在y轴上的椭圆,∴3-t>t+1>0,
解得:-1<t<1.
(2)∵命题P是命题q的充分不必要条件,
∴-1<t<1是不等式t2-(a-1)t-a<0解集的真子集,
因方程t2-(a-1)t-a=0的两根为-1,-a.
故只需a>1.
点评 本题考查了简易逻辑的判定方法、一元二次不等式的解法、椭圆的标准方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.“?x∈R,x02-x0+1≤0”的否定是( )
| A. | ?x∈R,x02-x0+1<0 | B. | ?x∈R,x02-x0+1<0 | C. | ?x∈R,x02-x0+1≥0 | D. | ?x∈R,x02-x0+1>0 |
10.已知函数y=$\frac{\sqrt{2-x}}{{x}^{2}-9}$,其定义域为( )
| A. | (-∞,2) | B. | (-∞,2] | C. | (-∞,-3)∪(-3,2] | D. | [2,3)∪(3,+∞) |
7.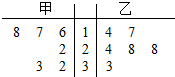 甲、乙两位运动员6场比赛的茎叶图如图所示,记甲、乙的平均成绩分别为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,下列判断正确的是( )
甲、乙两位运动员6场比赛的茎叶图如图所示,记甲、乙的平均成绩分别为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,下列判断正确的是( )
 甲、乙两位运动员6场比赛的茎叶图如图所示,记甲、乙的平均成绩分别为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,下列判断正确的是( )
甲、乙两位运动员6场比赛的茎叶图如图所示,记甲、乙的平均成绩分别为$\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$,下列判断正确的是( )| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,甲比乙成绩稳定 | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,乙比甲成绩稳定 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,乙比甲成绩稳定 |