Question

【题目】设△ABC的三内角A、B、C的对边分别是a、b、c，且b（sinB﹣sinC）+（c﹣a）（sinA+sinC）=0 （Ⅰ）求角A的大小；
（Ⅱ）若a= ，sinC= sinB，求△ABC的面积．

Answer 1

【答案】解：（Ⅰ）因为b（sinB﹣sinC）+（c﹣a）（sinA+sinC）=0， 由正弦定理得b（b﹣a）+（c﹣a）（a+c）=0，∴b2+c2﹣a2=bc，
∴由余弦定理得 ，∴在△ABC中， ．
（Ⅱ）方法一：因为 ，且 ，∴
∴ ，∴tanB=1，在△ABC中，
又在△ABC中，由正弦定理得 ，∴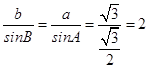
∴△ABC的面积
方法二：因为 ，由正弦定理得
而 ， ，由余弦定理得b2+c2﹣bc=a2 ， ∴
∴b2=2，即 ，
∴△ABC的面积S= =
【解析】（Ⅰ）由正弦定理得b2+c2﹣a2=bc，由由余弦定理求角A的大小；（Ⅱ）若a= ，sinC= sinB，利用三角形的面积公式，即可求△ABC的面积．