题目内容
函数y=
arcsin(2x-1)的值域是
| 1 |
| 2 |
[-
,
]
| π |
| 4 |
| π |
| 4 |
[-
,
]
.| π |
| 4 |
| π |
| 4 |
分析:根据-
≤arcsin(2x-1)≤
,可得-
≤
arcsin(2x-1)≤
,即得答案.
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
解答:解:由于当-1≤2x-1≤1时,由反正弦函数的定义可得-
≤arcsin(2x-1)≤
,
∴-
≤
arcsin(2x-1)≤
,
故答案为:[-
,
].
| π |
| 2 |
| π |
| 2 |
∴-
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
故答案为:[-
| π |
| 4 |
| π |
| 4 |
点评:本题主要考查反正弦函数的定义,不等式性质的应用,利用-
≤arcsin(2x-1)≤
,是解题的关键.
| π |
| 2 |
| π |
| 2 |

练习册系列答案
相关题目
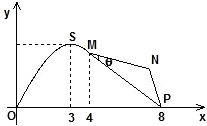 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为