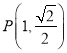题目内容
【题目】定义在（0，+∞）上的函数f（x）的导数
满足x2＜1，则下列不等式中一定成立的是（ ）
A.f（
）+1＜f（
）＜f（
）﹣1B.f（）+1＜f（）＜f（）﹣1
C.f（）﹣1＜f（）＜f（）+1D.f（）﹣1＜f（）＜f（）+1
【答案】D
【解析】
构造函数g（x）＝f（x）
，利用导数可知函数在（0，+∞）上是减函数，则答案可求．
由x2f′（x）＜1，得f′（x）
，即得f′（x）
0，
令g（x）＝f（x），则g′（x）＝f′（x）0，
∴g（x）＝f（x）在（0，+∞）上为单调减函数，
∴f（
）+2＜f（
）+3＜f（
）+4，
则f（）＜f（）+1，即f（）﹣1＜f（）；
f（）＜f（）+1．
综上，f（）﹣1＜f（）＜f（）+1．
故选：D．
世纪百通期末金卷系列答案
【题目】在2018年3月郑州第二次模拟考试中，某校共有100名文科学生参加考试，其中语文考试成绩低于130的占95%人，数学成绩的频率分布直方图如图：
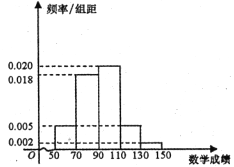
（Ⅰ）如果成绩不低于130的为特别优秀，这100名学生中本次考试语文、数学成绩特别优秀的大约各多少人？
（Ⅱ）如果语文和数学两科都特别优秀的共有3人．
（ⅰ）从（Ⅰ）中的这些同学中随机抽取2人，求这两人两科成绩都优秀的概率．
（ⅱ）根据以上数据，完成
列联表，并分析是否有99%的把握认为语文特别优秀的同学，数学也特别优秀．
语文特别优秀 | 语文不特别优秀 | 合计 | |
数学特别优秀 | |||
数学不特别优秀 | |||
合计 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关，在某医院随机对心肺疾病入院的
人进行问卷调查，得到了如下的列联表：
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
（1）用分层抽样的方法在患心肺疾病的人群中抽
人，其中男性抽多少人？
（2）在上述抽取的
人中选
人，求恰好有
名女性的概率；
（3）为了研究心肺疾病是否与性别有关，请计算出统计量
，你有多大把握认为心肺疾病与性别有关？
下面的临界值表供参考：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式： 
，其中
.
