题目内容
抛物线y2=2px的焦点与双曲线 的右焦点重合,则p的值为
的右焦点重合,则p的值为
- A.-2
- B.2
- C.-4
- D.4
D
分析:由题意抛物线y2=2px的焦点与双曲线 的右焦点重合,可先解出双曲线的右焦点,从而得出
的右焦点重合,可先解出双曲线的右焦点,从而得出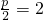 ,解出p的值,即可选出正确选项
,解出p的值,即可选出正确选项
解答:由于双曲线 可得a=
可得a= ,b=1,故可得c=2
,b=1,故可得c=2
由双曲线方程的形式知,其右焦点坐标是(2,0)
又抛物线y2=2px的焦点与双曲线 的右焦点重合
的右焦点重合
∴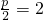 ,得p=4
,得p=4
故选D
点评:本题考查圆锥曲线的共同特征,解题的关键是理解圆锥曲线的方程与a,b,c,p的关系,由此建立方程解出参数的值,本题考查了方程的思想及推理判断的能力
分析:由题意抛物线y2=2px的焦点与双曲线
 的右焦点重合,可先解出双曲线的右焦点,从而得出
的右焦点重合,可先解出双曲线的右焦点,从而得出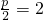 ,解出p的值,即可选出正确选项
,解出p的值,即可选出正确选项解答:由于双曲线
 可得a=
可得a= ,b=1,故可得c=2
,b=1,故可得c=2由双曲线方程的形式知,其右焦点坐标是(2,0)
又抛物线y2=2px的焦点与双曲线
 的右焦点重合
的右焦点重合∴
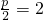 ,得p=4
,得p=4故选D
点评:本题考查圆锥曲线的共同特征,解题的关键是理解圆锥曲线的方程与a,b,c,p的关系,由此建立方程解出参数的值,本题考查了方程的思想及推理判断的能力

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
若抛物线y2=2px的焦点与双曲线
2-y2=1的右焦点重合,则p的值为( )
| x |
| 3 |
A、2
| ||
| B、4 | ||
| C、-4 | ||
| D、2 |