题目内容
 (2012•芜湖二模)如图,四棱锥P-ABCD的底面是正方形,PD⊥面ABCD,E是PD上一点.
(2012•芜湖二模)如图,四棱锥P-ABCD的底面是正方形,PD⊥面ABCD,E是PD上一点.(1)求证:AC⊥BE.
(2)若PD=AD=1,且∠PCE的余弦值为
3
| ||
| 10 |
分析:(1)连接BD,由已知中四棱锥P-ABCD的底面是正方形,PD⊥面ABCD,可得PD⊥AC,进而得到AC⊥面PBD,由线面平行的定义,可得答案.
(2)设PE=x,由勾股定理求出CE,结合∠PCE的余弦值为
,由余弦定理可得x值,代入棱锥体积公式可得答案.
(2)设PE=x,由勾股定理求出CE,结合∠PCE的余弦值为
3
| ||
| 10 |
解答:解:(1)连接BD
∵ABCD是正方形
∴AC⊥BD又PD⊥面ABCD
∴PD⊥AC
∵PD∩BD=D
∴AC⊥面PBD,又BE?面PBD
∴AC⊥BE…(6分)
(2)设PE=x,则CE=
=
又PC=
cos∠PCE=
∴△PCE中,由余弦定理解为:x=
∴S△PCE=
•PE•CD=
∴VE-PBC=VB-PCE=
•BCS△PCE=
•1•
=
…(12分)
∵ABCD是正方形
∴AC⊥BD又PD⊥面ABCD
∴PD⊥AC
∵PD∩BD=D
∴AC⊥面PBD,又BE?面PBD
∴AC⊥BE…(6分)
(2)设PE=x,则CE=
| DE2+CD2 |
| (1-x)2+1 |
又PC=
| 2 |
| 3 | ||
|
∴△PCE中,由余弦定理解为:x=
| 1 |
| 2 |
∴S△PCE=
| 1 |
| 2 |
| 1 |
| 4 |
∴VE-PBC=VB-PCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
点评:(1)的关键是于熟练掌握线面垂直,线线垂直之间的相互转化,熟练掌握线面垂直的定义及判定是基础;
(2)的关键是利用等积法,将三棱锥转化为B-PEC,解三角形PEC求出底面面积
(2)的关键是利用等积法,将三棱锥转化为B-PEC,解三角形PEC求出底面面积

练习册系列答案
相关题目
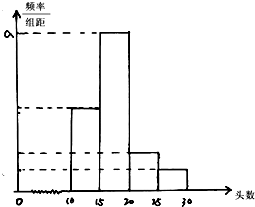 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: