题目内容
正四棱锥P﹣ABCD的所有棱长均相等,E是PC的中点,那么异面直线BE与PA所成的角的余弦值等于 .


考点: 异面直线及其所成的角.
专题: 空间角.
分析: 根据异面直线所成角的定义先找出对应的平面角即可得到结论.
解答: 解:连结AC,BD相交于O,
则O为AC的中点,
∵E是PC的中点,
∴OE是△PAC的中位线,
则OE∥ ,
,
则OE与BE所成的角即可异面直线BE与PA所成的角,
设四棱锥的棱长为1,
则OE= =
= ,OB=
,OB= ,BE=
,BE= ,
,
则cos =
= =
= ,
,
故答案为:


练习册系列答案
相关题目
 ,且
,且 //(
//( ),则k=______.
),则k=______.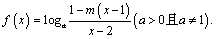
 时,判断
时,判断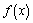 在
在 上的单调性,并说明理由;
上的单调性,并说明理由; ,
,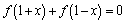 恒成立,求实数
恒成立,求实数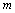 的值;
的值;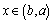 时,
时,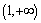 ,求实数
,求实数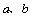 的值.
的值.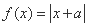 (
(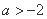 )的图象过点
)的图象过点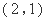 .
.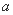 的值;
的值;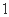 .试在该坐标系中作出函数
.试在该坐标系中作出函数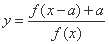 的简图,并写出(不需要证明)它的定义域、值域、奇偶性、单调区间.
的简图,并写出(不需要证明)它的定义域、值域、奇偶性、单调区间. 
 ,B=
,B= ,若BA=
,若BA= ,则x=
,则x= 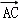 =(1,2),
=(1,2),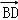 =(﹣4,2),则该四边形的面积为( )
=(﹣4,2),则该四边形的面积为( )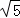 B.
B. 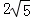 C. 5 D. 10
C. 5 D. 10 圈上的两点,它们的经度差为
圈上的两点,它们的经度差为 ,则A 、B两点间的球面距离为__
,则A 、B两点间的球面距离为__ 干组,
干组, 是其中一组,已知该组的频率为
是其中一组,已知该组的频率为 ,该组上的直方图的高为
,该组上的直方图的高为 ,则
,则 等于__________
等于__________