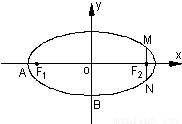
题目内容
已知椭圆C的左、右焦点坐标分别是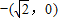
，
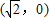，离心率是
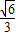，直线y=t椭圆C交与不同的两点M，N，以线段MN为直径作圆P，圆心为P．（Ⅰ）求椭圆C的方程；
（Ⅱ）若圆P与x轴相切，求圆心P的坐标．
【答案】分析：（Ⅰ）直接利用左、右焦点坐标和离心率是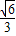
，就可求出对应椭圆C的方程；
（Ⅱ）先把直线y=t与椭圆C的方程求出点M，N的横坐标，进而求出圆的半径，再利用圆P与x轴相切就可求出t以及圆心P的坐标．
解答：解：（Ⅰ）因为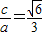
，且
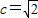，所以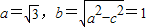
所以椭圆C的方程为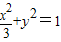
（Ⅱ）由题意知p（0，t）（-1＜t＜1）
由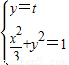
得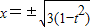
所以圆P的半径为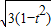
解得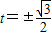
所以点P的坐标是（0，
）
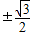点评：在求椭圆的标准方程时，一般是利用条件先求a，c，或b，c；再利用a，b，c之间的关系即可求出椭圆的标准方程．
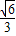，就可求出对应椭圆C的方程；（Ⅱ）先把直线y=t与椭圆C的方程求出点M，N的横坐标，进而求出圆的半径，再利用圆P与x轴相切就可求出t以及圆心P的坐标．
解答：解：（Ⅰ）因为
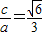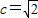，且，所以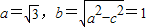所以椭圆C的方程为
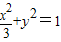
（Ⅱ）由题意知p（0，t）（-1＜t＜1）
由
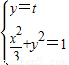得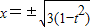所以圆P的半径为
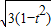
解得
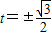所以点P的坐标是（0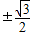，）点评：在求椭圆的标准方程时，一般是利用条件先求a，c，或b，c；再利用a，b，c之间的关系即可求出椭圆的标准方程．
练习册系列答案
相关题目
如图，在直角坐标系xOy中，已知椭圆C：
的离心率e＝
，左右两个焦分别为F1、F2．过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点，且|MN|＝1．
，(
)试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上.
+
=1（a＞b＞0）的离心率e=
，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的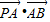
=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．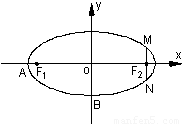
+
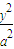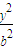=1（a＞b＞0）的离心率e=
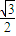，左右两个焦分别为F1、F2．过右焦点F2且与轴垂直的
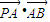=m-4，（m∈R）试求点P的轨迹方程，使点B关于该轨迹的对称点落在椭圆C上．