题目内容
 如图,一条直角走廊宽为1.5m,一转动灵活的平板手推车,其平板面为矩形,宽为1m.问:要想顺利通过直角走廊,平板手推车的长度不能超过
如图,一条直角走廊宽为1.5m,一转动灵活的平板手推车,其平板面为矩形,宽为1m.问:要想顺利通过直角走廊,平板手推车的长度不能超过分析:如图,先设平板手推车的长度不能超过 x米,则得出x为最大值时,此时平板手推车所形成的三角形:ADE'为等腰直角三角形.连接E与E'与AD交于点F,利用ADE'为等腰直角三角形即可求得平板手推车的长度不能超过多少米.
解答: 解:平板手推车的长度不能超过 x米,
解:平板手推车的长度不能超过 x米,
则此时x为最大值,且此时平板手推车所形成的三角形:
ADE'为等腰直角三角形.
连接E与E'与AD交于点F,得:EE'=(3
)/2
故:FE'=EE'-EF=(3
)/2-1
又ADE'为等腰直角三角形
故得:AD=2AF=2FE'=3
-2.
故答案为:3
-2.
 解:平板手推车的长度不能超过 x米,
解:平板手推车的长度不能超过 x米,则此时x为最大值,且此时平板手推车所形成的三角形:
ADE'为等腰直角三角形.
连接E与E'与AD交于点F,得:EE'=(3
| 2 |
故:FE'=EE'-EF=(3
| 2 |
又ADE'为等腰直角三角形
故得:AD=2AF=2FE'=3
| 2 |
故答案为:3
| 2 |
点评:本题主要考查了在实际问题中建立三角函数模型,解答的关键是由题意得出要想顺利通过直角走廊,此时平板手推车所形成的三角形为等腰直角三角形.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 如图,一条直角走廊宽为1.5m,一转动灵活的平板推车,其平板面为矩形,宽为1m.问:要想顺利通过直角走廊,平板推车的长度BC不能超过多少米?
如图,一条直角走廊宽为1.5m,一转动灵活的平板推车,其平板面为矩形,宽为1m.问:要想顺利通过直角走廊,平板推车的长度BC不能超过多少米?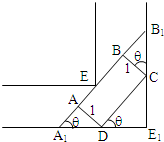 一条直角走廊宽 1.5米,如图所示,现有一转动灵活的手推车,其平板面为矩形ABCD,宽AD为1米,延长AB交直角走廊于A1、B1,设∠CDE1=θ,
一条直角走廊宽 1.5米,如图所示,现有一转动灵活的手推车,其平板面为矩形ABCD,宽AD为1米,延长AB交直角走廊于A1、B1,设∠CDE1=θ,
