题目内容
若方程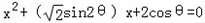 (其中0<θ<π)的两实根为α、β,数列1,
(其中0<θ<π)的两实根为α、β,数列1,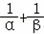 ,
,
(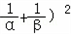 ,…的所有项的和为2﹣
,…的所有项的和为2﹣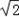 ,试求θ的值.
,试求θ的值.
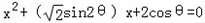 (其中0<θ<π)的两实根为α、β,数列1,
(其中0<θ<π)的两实根为α、β,数列1,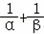 ,
,(
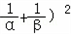 ,…的所有项的和为2﹣
,…的所有项的和为2﹣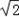 ,试求θ的值.
,试求θ的值.解:∵方程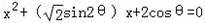 (其中0<θ<π)的两实根为α、β,
(其中0<θ<π)的两实根为α、β,
∴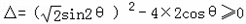 (1)
(1)
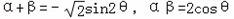
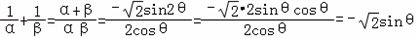 ,
,
由已知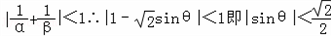
而θ∈(0,π)∴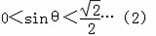
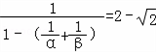 ∴
∴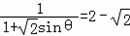
∴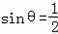 满足(2)
满足(2)
∴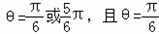 不满足(1)
不满足(1)
故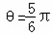
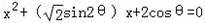 (其中0<θ<π)的两实根为α、β,
(其中0<θ<π)的两实根为α、β,∴
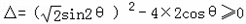 (1)
(1)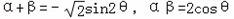
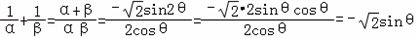 ,
,由已知
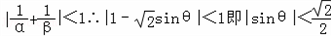
而θ∈(0,π)∴
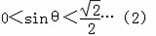
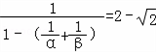 ∴
∴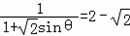
∴
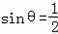 满足(2)
满足(2)∴
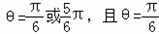 不满足(1)
不满足(1)故
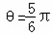

练习册系列答案
相关题目
 x∈R成立;
x∈R成立; x∈R成立;
x∈R成立; 为坐标原点,已知两点
为坐标原点,已知两点 ,
, ,若点
,若点 满足
满足 其中0≤
其中0≤ ≤1,且
≤1,且 ,则点
,则点 B.
B.
 (
( ) D.
) D. (
( (其中0<θ<π)的两实根为α、β,数列1,
(其中0<θ<π)的两实根为α、β,数列1, ,(
,( ,…的所有项的和为2-
,…的所有项的和为2- ,试求θ的值.
,试求θ的值.