题目内容
已知椭圆M的两个焦点分别为F1(-1,0),F2(1,0),P是椭圆上的一点,且PF1⊥PF2,|PF1|·|PF2|=8.(1)求椭圆M的方程;
(2)点A是椭圆M短轴的一个端点,且其纵坐标大于零,点B、C是椭圆M上不同于点A的两点,其中△ABC的重心是椭圆M的右焦点,求直线BC的方程.
解:(1)设|PF1|=m,|PF2|=n,由已知得mn=8,由PF1⊥PF2,得m2+n2=4,
∴(m+n)2=m2+n2+2mn=20,即(2a)2=20,得a2=5.
∴b2=a2-c2=4.
故椭圆M的方程为![]() +
+![]() =1.
=1.
(2)设B(x1,y1),C(x2,y2),直线BC的斜率为k,BC中点为(x0,y0),A(0,2).
显然BC不会与x轴垂直,故x1≠x2,
则![]() +
+![]() =1, ①
=1, ①
![]() +
+![]() =1, ②
=1, ②
①-②得![]() =
=![]() . ③
. ③
由于F2(1,0)是△ABC的重心,
所以![]() =1,得x0=
=1,得x0=![]() =
=![]() ,
,![]() =0,得y0=
=0,得y0=![]() =-1,
=-1,
代入③得k=![]() ,
,
∴直线BC的方程为6x-5y-14=0.

练习册系列答案
相关题目
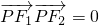 ,
,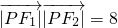 .
. ,
, .
.