题目内容
已知椭圆M的两个焦点分别为F1(-1,0),F2(1,0),P是此椭圆上的一点,且
•
=0,
•
=8.
(1)求椭圆M的方程;
(2)点A是椭圆M短轴的一个端点,且其纵坐标大于零,B、C是椭圆上不同于点A的两点,若△ABC的重心是椭圆的右焦点,求直线BC的方程.
| PF1 |
| PF2 |
| |PF1| |
| |PF2| |
(1)求椭圆M的方程;
(2)点A是椭圆M短轴的一个端点,且其纵坐标大于零,B、C是椭圆上不同于点A的两点,若△ABC的重心是椭圆的右焦点,求直线BC的方程.
(1)设|
|=m,|
| =n,
由
,
∴a=
,c=1,b=2,
∴
+
=1.
(2)设B(x1,y1),C(x2,y2),A(0,2),
由重心公式,得
,
∴线段BC的中点为D(
,-1),
将点B,C代入椭圆方程,再相减,
得
+
=0,
∴k=
,
由点斜式得6x-5y-14=0.
| PF1 |
| PF2 |
由
|
∴a=
| 5 |
∴
| x2 |
| 5 |
| y2 |
| 4 |
(2)设B(x1,y1),C(x2,y2),A(0,2),
由重心公式,得
|
∴线段BC的中点为D(
| 3 |
| 2 |
将点B,C代入椭圆方程,再相减,
得
| (x1+x2)(x1-x2) |
| 5 |
| (y1+y2)(y1-y2) |
| 4 |
∴k=
| 6 |
| 5 |
由点斜式得6x-5y-14=0.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
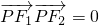 ,
,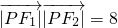 .
. ,
, .
.