题目内容
已知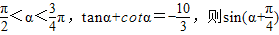 = .
= .
【答案】分析:根据同角三角函数的关系化简已知等式,得到sinαcosα=-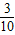 ,从而(sinα+cosα)2=1+2sinαcosα=
,从而(sinα+cosα)2=1+2sinαcosα= ,结合α的范围解出sinα+cosα=-
,结合α的范围解出sinα+cosα=-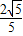 ,再由两角和的正弦公式即可得到sin(α+
,再由两角和的正弦公式即可得到sin(α+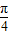 )=
)=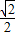 (sinα+cosα)=-
(sinα+cosα)=-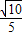 .
.
解答:解:∵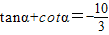
∴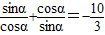 ,可得
,可得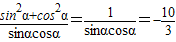
因此,sinαcosα=-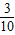
∴(sinα+cosα)2=1+2sinαcosα= ,
,
∵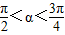 ,可得sinα+cosα<0
,可得sinα+cosα<0
∴sinα+cosα=-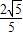 ,
,
可得sin(α+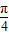 )=
)=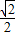 (sinα+cosα)=
(sinα+cosα)=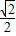 ×(-
×(-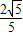 )=-
)=-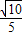
故答案为:-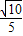
点评:本题给出三角函数等式,求sin(α+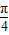 )的值.着重考查了两角和的正弦公式和同角三角函数的关系等知识,属于中档题.
)的值.着重考查了两角和的正弦公式和同角三角函数的关系等知识,属于中档题.
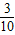 ,从而(sinα+cosα)2=1+2sinαcosα=
,从而(sinα+cosα)2=1+2sinαcosα= ,结合α的范围解出sinα+cosα=-
,结合α的范围解出sinα+cosα=-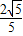 ,再由两角和的正弦公式即可得到sin(α+
,再由两角和的正弦公式即可得到sin(α+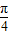 )=
)=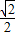 (sinα+cosα)=-
(sinα+cosα)=-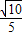 .
.解答:解:∵
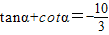
∴
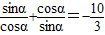 ,可得
,可得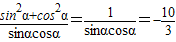
因此,sinαcosα=-
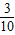
∴(sinα+cosα)2=1+2sinαcosα=
 ,
,∵
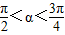 ,可得sinα+cosα<0
,可得sinα+cosα<0∴sinα+cosα=-
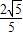 ,
,可得sin(α+
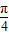 )=
)=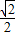 (sinα+cosα)=
(sinα+cosα)=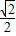 ×(-
×(-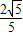 )=-
)=-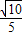
故答案为:-
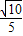
点评:本题给出三角函数等式,求sin(α+
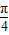 )的值.着重考查了两角和的正弦公式和同角三角函数的关系等知识,属于中档题.
)的值.着重考查了两角和的正弦公式和同角三角函数的关系等知识,属于中档题. 
练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力.每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%.假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
(Ⅰ)任选1名下岗人员,求该人参加过培训的概率;
(Ⅱ)任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.
| ξ | 0 | 1 | 2 | 3 |
| P | 0.021 | 0.027 | 0.243 | 0.729 |
已知函数f(x)=-x3+ax2-x-1在(-∞,+∞)上是单调函数,则实数a的取值范围是( )
A、(-∞,-
| ||||
B、[-
| ||||
C、(-∞,-
| ||||
D、(-
|
已知函数f(x)=
若f(2-a2)>f(a),则实数a的取值范围是( )
|
| A、(-∞,-1)∪(2,+∞) |
| B、(-1,2) |
| C、(-2,1) |
| D、(-∞,-2)∪(1,+∞) |