题目内容
如图,平面α与平面β相交成锐角θ,平面α内的一个圆在平面β上的射影是离心率为
的椭圆,则角θ等于______.
| 1 |
| 2 |

由题意可得:平面α上的一个圆在平面β上的射影是一个离心率为
的椭圆,也可以说为:β上的一个离心率为
的椭圆在α上的射影是一个圆,
设圆的半径为r,所以b=r,
又因为
=
,并且b2=a2-c2,所以a=
r.
所以cosθ=
=
,所以θ=30°.
故答案为:30°
| 1 |
| 2 |
| 1 |
| 2 |
设圆的半径为r,所以b=r,
又因为
| c |
| a |
| 1 |
| 2 |
2
| ||
| 3 |
所以cosθ=
| 2r |
| 2a |
| ||
| 2 |
故答案为:30°

练习册系列答案
相关题目

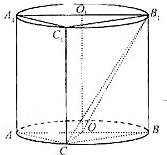 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.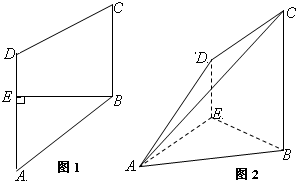 (2013•威海二模)如图1,在梯形ABCD中,BC∥DA,BE⊥DA,EA=EB=BC=2,DE=1,将四边形DEBC沿BE折起,使平面DEBC垂直平面ABE,如图2,连结AD,AC.
(2013•威海二模)如图1,在梯形ABCD中,BC∥DA,BE⊥DA,EA=EB=BC=2,DE=1,将四边形DEBC沿BE折起,使平面DEBC垂直平面ABE,如图2,连结AD,AC. (Ⅰ)求直三棱柱ABC-A′B′C′的体积;
(Ⅰ)求直三棱柱ABC-A′B′C′的体积; 如图,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )
如图,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( )