题目内容
在平行六面体ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=4,AD=3,AA1=5,∠BAD=60°,则AC1的长为多少?.
 解:由题意,AC2=AB2+BC2-2AB•BCcos120°=32+42-2×3×4×cos120°=3
解:由题意,AC2=AB2+BC2-2AB•BCcos120°=32+42-2×3×4×cos120°=3因为AA1⊥底面ABCD,
∴△ACC1是直角三角形,
∴AC12=AC2+CC12=37+25=62
∴AC1的长是
 .
.分析:先利用余弦定理求AC,再利用侧棱垂直于底面,从而可求体对角线长.
点评:本题主要考查了体对角线的求解,以及余弦定理的应用,同时考查了空间想象能力,计算推理的能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
如图,在平行六面体ABCD-A1B1C1D1中,O为AC与BD的交点,若
=
,
=
,
=
,则向量
等于( )
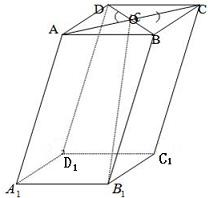
| A1B1 |
| a |
| A1D1 |
| b |
| AA1 |
| c |
| B1O |

A、
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、-
|
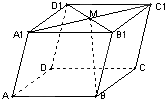 如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若
如图:在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| BM |
A、-
| ||||||||||
B、
| ||||||||||
C、-
| ||||||||||
D、
|
 已知在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,且∠BAD=∠BAA1=∠DAA1=60°,求AC1的长.
已知在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,且∠BAD=∠BAA1=∠DAA1=60°,求AC1的长.