Question

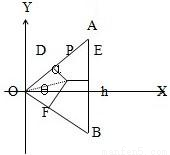
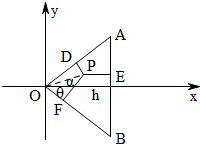设等腰△OAB的顶点为2θ，高为h．
（1）在△OAB内有一动点P，到三边OA，OB，AB的距离分别为|PD|，|PF|，|PE|，并且满足关系|PD|•|PF|=|PE|²，求P点的轨迹．
（2）在上述轨迹中定出点P的坐标，使得|PD|+|PE|=|PF|．

Answer 1

分析：（1）设OP与正X轴的夹角为α，P的坐标为（x，y），由题意知|OP|=

x2+y2

，|PD|=xsinθ-ycosθ，|PF|=xsinθ+ycosθ，由条件|PD|×|PF|=|PE|²得x²cos²θ-2hx+y²cos²θ+h²=0，由此可知x(x-

h

cos2θ

)2+y2=(h

sinθ

cos2θ

)2，所求轨迹是此圆在所给等腰三角形内的一部分．
（2）由题意知x²sin²θ-y²cos²θ=4y²cos²θ，所以5y³cos²θ=x²sin²θ，y=

1

5

tgθ•x，由此入手可以推出所求点P的坐标．

解答：解：（1）设OP与正X轴的夹角为α，P的坐标为（x，y），
则|OP|=

x2+y2

|PD|=|OP|sin（θ-α）=|OP|（sinθcosα-cosθsinα）=xsinθ-ycosθ
|PF|=|OP|sin（θ+α）=|OP|（sinθcosα+cosθsinα）=xsinθ+ycosθ
由条件|PD|×|PF|=|PE|²得x²sin²θ-y²cos²θ=（h-x）²（1）
即x²cos²θ-2hx+y²cos²θ+h²=0
除以cos²θ≠0得x2-

2h

cos2θ

x+y2+

h2

cos2θ

=0
即x(x-

h

cos2θ

)2+y2=(h

sinθ

cos2θ

)2
这是以(

h

cos2θ

，0)为中心，以h

sinθ

cos2θ

为半径的圆，所求轨迹是此圆在所给等腰三角形内的一部分，
注意：在A作直线AE′⊥OA，则OE′=

h

cos2θ

，E′是圆的中心AE′=h

sinθ

cos2θ

是圆的半径，A是圆上一点，而且圆在A的切线是OA．

（2）由条件|PD|+|PE|=|PF|得xsinθ-ycosθ+h-x=xsinθ+ycosθ
即x+ycosθ=h （2）此直线通过（h，0）点及（0，

h

2cosθ

）点，
由（1），（2）得x²sin²θ-y²cos²θ=4y²cos²θ，
∴5y³cos²θ=x²sin²θ，
y=

1

5

tgθ•x
由|PD|+|PE|=|PF|可知y＞0，所以这里右端取正号，
代入（2）得x(1+

2

5

sinθ)=h，
∴x=

h

1+ 2 5 sinθ

=

5 h

5 +2sinθ

，
y=

1

5

•

5 h

5 +2sinθ

tgθ=

htgθ

5 +2sinθ

，
所求点P的坐标为（

5 h

5 +2sinθ

，

htgθ

5 +2sinθ

）．

点评：本题二圆锥曲线知识的综合运用，解题时要认真审题，仔细解答．