题目内容
【题目】已知M为△ABC的中线AD的中点,过点M的直线分别交两边AB、AC于点P、Q,设 ![]() =x
=x ![]() ,
, ![]() ,记y=f(x).
,记y=f(x).
(1)求函数y=f(x)的表达式;
(2)设g(x)=x3+3a2x+2a,x∈[0,1].若对任意x1∈[ ![]() ,1],总存在x2∈[0,1],使得f(x1)=g(x2)成立,求实数a的取值范围.
,1],总存在x2∈[0,1],使得f(x1)=g(x2)成立,求实数a的取值范围.
【答案】
(1)解:∵过点M的直线分别交两边AB、AC于P、Q,
∴0<x≤1,0<y≤1
又∵ ![]() =x
=x ![]() ,
, ![]() =y
=y ![]() ,
,
∴ ![]() =
= ![]()
![]() =
= ![]() (
( ![]() +
+ ![]() )=
)= ![]()
![]() +
+ ![]()
![]()
又∵P、M、Q三点共线,
∴ ![]() +
+ ![]() =1,
=1,
∴y=f(x)= ![]()
由 ![]() 得
得 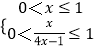 ,
,
∴ ![]() ≤x≤1,
≤x≤1,
∴y=f(x)= ![]() ,x∈[
,x∈[ ![]() ,1]
,1]
(2)解:∵f(x)= ![]() =
= ![]() +
+ ![]() 在[
在[ ![]() ,1]内是减函数,
,1]内是减函数,
∴[f(x)]min=f(1)= ![]() ,[f(x)]max=f(
,[f(x)]max=f( ![]() )=1,
)=1,
即函数f(x)的值域为[ ![]() ,1]
,1]
∵g'(x)=3x2+3a2≥0,
∴g(x)在[0,1]内是增函数,
∴[g(x)]min=g(0)=2a,[g(x)]max=g(1)=3a2+2a+1,
∴g(x)的值域为[2a,3a2+2a+1]
由题设得[ ![]() ,1][2a,3a2+2a+1],
,1][2a,3a2+2a+1],
则 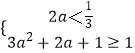
解得a的取值范围是(﹣∞,﹣ ![]() ]∪[0,
]∪[0, ![]() ]
]
【解析】(1)表示出向量AM,根据P、M、Q三点共线,得到关于x,y的等式,解出y即f(x)的解析式;(2)分别根据f(x),g(x)的单调性,求出f(x),g(x)的值域,结合集合的包含关系得到关于a的不等式组,解出即可.
【考点精析】掌握平面向量的基本定理及其意义是解答本题的根本,需要知道如果![]() 、
、![]() 是同一平面内的两个不共线向量,那么对于这一平面内的任意向量
是同一平面内的两个不共线向量,那么对于这一平面内的任意向量![]() ,有且只有一对实数
,有且只有一对实数![]() 、
、![]() ,使
,使![]() .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目