题目内容
已知圆O：
上的点到直线
的最小距离为1，设P为直线
上的点，过P点作圆O的两条切线PA、PB， 其中A、B为切点.
（1）求圆O的方程；
（2）当点P
为直线上的定点时，求直线AB的方程.
（1）
；（2）
.
【解析】
试题分析：（1）圆上的点到直线的最小距离是圆心到直线的距离减去圆的半径，这样就求得了半径的值；
（2）先设出两个切点坐标
，有四个坐标变量来表示两条切线方程，两条切线都过点
，整理出关系式
，再表示出直线AB的方程，消去变量
整理就得到了
.
试题解析：（1）圆心到直线的距离
（2）设 
，
由于
，有
那么直线AB：
，即 
考点：直线方程与圆的方程.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
B．
C．
D．
，则目标函数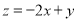
的最大值是（ ）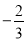
发出的光线，沿平行于抛物线
的对称轴方向射向此抛物线上的点
，经抛物线反射后，穿过焦点射向抛物线上的点
，再经抛物线反射后射向直线
上的点
，经直线反射后又回到点
，则
等于（ ）
B．
C．
D．
，q:
，若q是p的必要而不充分条件，
B．
C.
D．
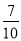为概率的事件是
中, 
,则
= ． 
满足
，若离心率为
，则
的最小值为_______.