题目内容
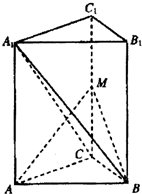 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA= ,AA1=
,AA1= M为侧棱CC1上一点,AM⊥A1C;
M为侧棱CC1上一点,AM⊥A1C;
(1)求证:B1C1∥平面A1BC;
(2)求异面直线A1B与AC所成的角的余弦值;
(3)求点C到平面ABM的距离.
解:(1)证明:在直棱柱ABC-A1B1C1中,
B1C1∥BC,B1C1?平面A1BC,BC?平面A1BC
∴B1C1∥平面A1BC.
(2)在直棱柱ABC-A1B1C1中,AC∥A1C1,
∴∠BA1C1或其补角是异面直线A1B与AC所成的角.
连接BC1,
∴CC1⊥平面A1B1C1,
∴CC1⊥A1C1,
又∠A1C1B1=∠ACB=90°,即A1C1⊥B1C1
∴A1C1⊥平面BB1C1C,
∴BC1?平面BB1C1C,
∴A1C1⊥BC1,
在Rt△BCC1中,BC=1,CC1=AA1= ,
,
∴BC1=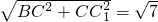
在Rt△ABC1中,A1C1= ,BC1=
,BC1= ,
,
∴A1B=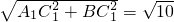
∴ .
.
(3)过点C作CD⊥AB于N,连接MD,过点C作CH⊥MD于H,
∵CC1⊥平面ABC,
∴由三垂线定理,得MD⊥AB,
∴AB⊥平面MCD,
∴AB⊥CH,又CH⊥MD,
∴CH⊥平面ABM,即CH为点C到平面ABM的距离.
在平面A1ACC1中,由A1C⊥AM,易得△A1AC∽△ACM,
∴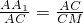 ,
,
∴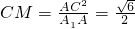 ,
,
在Rt△ABC中,AB=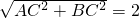 .
.
∴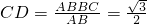 ,
,
∴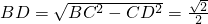 ,
,
在Rt△MCD中,MD=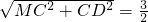 .
.
∴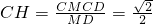 .
.
分析:(1)利用直棱柱的性质说明B1C1∥BC,B1C1?平面A1BC,BC?平面A1BC,即可证明B1C1∥平面A1BC.
(2)说明∠BA1C1或其补角是异面直线A1B与AC所成的角.连接BC1,求出BC1= ,在Rt△ABC1中,求出
,在Rt△ABC1中,求出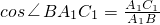 的值即可.
的值即可.
(3)过点C作CD⊥AB于N,连接MD,过点C作CH⊥MD于H,说明CH为点C到平面ABM的距离.
通过△A1AC∽△ACM,求出CM,在Rt△MCD中,求出MD,利用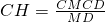 ,解出CH.
,解出CH.
点评:本题考查直线与平面的平行,异面直线所成的角,点到平面的距离的求法,找出异面直线所成的角与点到平面的距离是解题的关键,考查空间想象能力,计算能力.
B1C1∥BC,B1C1?平面A1BC,BC?平面A1BC
∴B1C1∥平面A1BC.
(2)在直棱柱ABC-A1B1C1中,AC∥A1C1,
∴∠BA1C1或其补角是异面直线A1B与AC所成的角.
连接BC1,
∴CC1⊥平面A1B1C1,
∴CC1⊥A1C1,
又∠A1C1B1=∠ACB=90°,即A1C1⊥B1C1
∴A1C1⊥平面BB1C1C,
∴BC1?平面BB1C1C,
∴A1C1⊥BC1,
在Rt△BCC1中,BC=1,CC1=AA1=
 ,
,∴BC1=
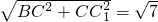
在Rt△ABC1中,A1C1=
 ,BC1=
,BC1= ,
,∴A1B=
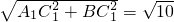
∴
 .
.(3)过点C作CD⊥AB于N,连接MD,过点C作CH⊥MD于H,
∵CC1⊥平面ABC,
∴由三垂线定理,得MD⊥AB,
∴AB⊥平面MCD,
∴AB⊥CH,又CH⊥MD,
∴CH⊥平面ABM,即CH为点C到平面ABM的距离.
在平面A1ACC1中,由A1C⊥AM,易得△A1AC∽△ACM,
∴
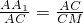 ,
,∴
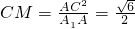 ,
,在Rt△ABC中,AB=
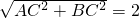 .
.∴
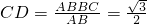 ,
,∴
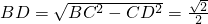 ,
,在Rt△MCD中,MD=
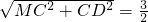 .
.∴
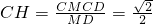 .
.分析:(1)利用直棱柱的性质说明B1C1∥BC,B1C1?平面A1BC,BC?平面A1BC,即可证明B1C1∥平面A1BC.
(2)说明∠BA1C1或其补角是异面直线A1B与AC所成的角.连接BC1,求出BC1=
 ,在Rt△ABC1中,求出
,在Rt△ABC1中,求出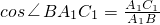 的值即可.
的值即可.(3)过点C作CD⊥AB于N,连接MD,过点C作CH⊥MD于H,说明CH为点C到平面ABM的距离.
通过△A1AC∽△ACM,求出CM,在Rt△MCD中,求出MD,利用
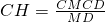 ,解出CH.
,解出CH.点评:本题考查直线与平面的平行,异面直线所成的角,点到平面的距离的求法,找出异面直线所成的角与点到平面的距离是解题的关键,考查空间想象能力,计算能力.

练习册系列答案
相关题目




