题目内容
【题目】设![]() ,
, ![]() 是椭圆
是椭圆![]() 上的两点,椭圆的离心率为
上的两点,椭圆的离心率为![]() ,短轴长为2,已知向量
,短轴长为2,已知向量![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆的焦点
过椭圆的焦点![]() ,(
,( ![]() 为半焦距),求直线
为半焦距),求直线![]() 的斜率
的斜率![]() 的值;
的值;
(2)试问: ![]() 的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据条件可得![]() ,再设直线
,再设直线![]() 的方程为:
的方程为: ![]() ,与椭圆联立方程组,利用韦达定理和已知条件
,与椭圆联立方程组,利用韦达定理和已知条件![]() ,即可求出
,即可求出![]() 的值;(2)先考虑直线
的值;(2)先考虑直线![]() 斜率不存在的情况,即
斜率不存在的情况,即![]() ,
, ![]() ,根据
,根据![]() ,求得
,求得![]() 和
和![]() 的关系式,代入椭圆的方程求得
的关系式,代入椭圆的方程求得![]() 点的横坐标和纵坐标的绝对值,进而求得△AOB的面积的值;当直线
点的横坐标和纵坐标的绝对值,进而求得△AOB的面积的值;当直线![]() 斜率存在时,设出直线
斜率存在时,设出直线![]() 的方程,与椭圆联立方程组,利用韦达定理表示出
的方程,与椭圆联立方程组,利用韦达定理表示出![]() 和
和![]() ,再利用
,再利用![]() ,弦长公式及三角形面积公式求得答案.
,弦长公式及三角形面积公式求得答案.
试题解析:(1)由题可得: ![]() ,
, ![]() ,所以,椭圆的方程为
,所以,椭圆的方程为![]()
设![]() 的方程为:
的方程为: ![]() ,代入
,代入![]() 得:
得: ![]()
∴![]() ,
, ![]() ,
, ![]()
∵![]() ,∴
,∴![]() ,即:
,即: 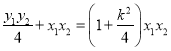
![]()
即![]() ,解得:
,解得: ![]()
(2)①直线![]() 斜率不存在时,即
斜率不存在时,即![]() ,
, ![]()
∵![]()
∴![]() ,即
,即![]()
又∵![]() 点在椭圆上
点在椭圆上
∴![]() ,即
,即![]()
∴![]() ,
, ![]()
∴![]() ,故
,故![]() 的面积为定值1
的面积为定值1
②当直线![]() 斜率存在时,设
斜率存在时,设![]() 的方程为
的方程为![]() ,
,
联立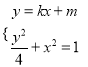 得:
得: ![]()
∴![]() ,
, ![]() ,
, ![]()
∴![]()
![]()
![]()
所以三角形的面积为定值1.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目