题目内容
设数列{an}是有穷等差数列,给出下面数表:a1 a2 a3 …an-1 an 第1行
a1+a2 a2+a3 …an-1+an 第2行
…
…
…第n行
上表共有n行,其中第1行的n个数为a1,a2,a3…an,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为b1,b2,b3…bn.
(1)求证:数列b1,b2,b3…bn成等比数列;
(2)若ak=2k-1(k=1,2,…,n),求和
 .
.
【答案】分析:(1)由题设易知,b1= ,b2=a1+an,容易得
,b2=a1+an,容易得 ,bk+1=c1+cn-k+1,于是
,bk+1=c1+cn-k+1,于是 ,可证明
,可证明
(2)由(1)求, =
= ,则ak=2k-1时,akbk=(2k-1)•2k-1,利用错位相减可求数列的和
,则ak=2k-1时,akbk=(2k-1)•2k-1,利用错位相减可求数列的和
解答:(1)证明:由题设易知, =
= ,
,
 =
= .
.
设表中的第k(1≤k≤n-1)行的数为c1,c2…cn-k+1,显然c1,c2…cn-k+1,成等差数列,则它的第k+1行的数是c1+c2,c2+c3…cn-k+cn-k+1也成等差数列,它们的平均数分别是 ,bk+1=c1+cn-k+1,于是
,bk+1=c1+cn-k+1,于是 (1≤k≤n-1,k∈N*).
(1≤k≤n-1,k∈N*).
故数列b1,b2…bn是公比为2的等比数列.(7分)
(2)由(1)知, =
= ,
,
故当ak=2k-1时, ,
, .
.
于是 n
n . (9分)
. (9分)
设 ,
,
则S=1•2+3•21+5•22+…+(2n-1)•2n-1①
2S=1•2+3×22+…+(2n-3)•2n-1+(2n-1)•2n②
①-②得,-S=1×2+2(2+22+…+2n-1)-(2n-1)•2n,
化简得,S=(2n-1)•2n-2n+1+3,
故 =n(2n-1)•2n-n•2n+1+3n.(14分)
=n(2n-1)•2n-n•2n+1+3n.(14分)
点评:本题主要考查了等比数列的定义在等比数列的证明中的应用,错位相减求解数列的和,解题的关键需要由已只条件中的信息提炼出相关的递推关系
 ,b2=a1+an,容易得
,b2=a1+an,容易得 ,bk+1=c1+cn-k+1,于是
,bk+1=c1+cn-k+1,于是 ,可证明
,可证明(2)由(1)求,
 =
= ,则ak=2k-1时,akbk=(2k-1)•2k-1,利用错位相减可求数列的和
,则ak=2k-1时,akbk=(2k-1)•2k-1,利用错位相减可求数列的和解答:(1)证明:由题设易知,
 =
= ,
, =
= .
.设表中的第k(1≤k≤n-1)行的数为c1,c2…cn-k+1,显然c1,c2…cn-k+1,成等差数列,则它的第k+1行的数是c1+c2,c2+c3…cn-k+cn-k+1也成等差数列,它们的平均数分别是
 ,bk+1=c1+cn-k+1,于是
,bk+1=c1+cn-k+1,于是 (1≤k≤n-1,k∈N*).
(1≤k≤n-1,k∈N*).故数列b1,b2…bn是公比为2的等比数列.(7分)
(2)由(1)知,
 =
= ,
,故当ak=2k-1时,
 ,
, .
.于是
 n
n . (9分)
. (9分)设
 ,
,则S=1•2+3•21+5•22+…+(2n-1)•2n-1①
2S=1•2+3×22+…+(2n-3)•2n-1+(2n-1)•2n②
①-②得,-S=1×2+2(2+22+…+2n-1)-(2n-1)•2n,
化简得,S=(2n-1)•2n-2n+1+3,
故
 =n(2n-1)•2n-n•2n+1+3n.(14分)
=n(2n-1)•2n-n•2n+1+3n.(14分)点评:本题主要考查了等比数列的定义在等比数列的证明中的应用,错位相减求解数列的和,解题的关键需要由已只条件中的信息提炼出相关的递推关系

练习册系列答案
相关题目

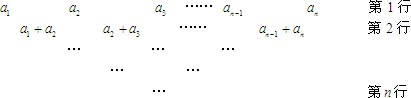

 .
.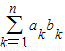 .
.