题目内容
设数列{an}是有穷等差数列,给出下面数表:

上表共有n行,其中第1行的n个数为a1,a2,a3…an,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为b1,b2,b3…bn. (1)求证:数列b1,b2,b3…bn成等比数列;
(2)若ak=2k﹣1(k=1,2,…,n),求和 .
.
(2)若ak=2k﹣1(k=1,2,…,n),求和
 .
.(1)证明:由题设易知, =
= ,
,
 =
= .
.
设表中的第k(1≤k≤n﹣1)行的数为c1,c2…cn﹣k+1,显然c1,c2…c n﹣k+1,成等差数列,
则它的第k+1行的数是c1+c2,c2+c3…c n﹣k+c n﹣k+1也成等差数列,
它们的平均数分别是 ,
,
b k+1=c1+c n﹣k+1,
于是 (1≤k≤n﹣1,k∈N*).
(1≤k≤n﹣1,k∈N*).
故数列b1,b2…bn是公比为2的等比数列.
(2)由(1)知, =
= ,
,
故当ak=2k﹣1时, ,
, .
.
于是 n
n .
.
设 ,则S=1×20+3×21+5×22+…+(2n﹣1)×2 n﹣1 ①
,则S=1×20+3×21+5×22+…+(2n﹣1)×2 n﹣1 ①
2S=12+3×22+…+(2n﹣3)×2 n﹣1+(2n﹣1)×2n ②
①﹣②得,﹣S=1×20+2(2+22+…+2 n﹣1)﹣(2n﹣1)2n,
化简得,S=(2n﹣1)2n﹣2 n+1+3,
故 =n(2n﹣1)×2n﹣n×2 n+1+3n.
=n(2n﹣1)×2n﹣n×2 n+1+3n.
 =
= ,
, =
= .
.设表中的第k(1≤k≤n﹣1)行的数为c1,c2…cn﹣k+1,显然c1,c2…c n﹣k+1,成等差数列,
则它的第k+1行的数是c1+c2,c2+c3…c n﹣k+c n﹣k+1也成等差数列,
它们的平均数分别是
 ,
,b k+1=c1+c n﹣k+1,
于是
 (1≤k≤n﹣1,k∈N*).
(1≤k≤n﹣1,k∈N*).故数列b1,b2…bn是公比为2的等比数列.
(2)由(1)知,
 =
= ,
,故当ak=2k﹣1时,
 ,
, .
.于是
 n
n .
. 设
 ,则S=1×20+3×21+5×22+…+(2n﹣1)×2 n﹣1 ①
,则S=1×20+3×21+5×22+…+(2n﹣1)×2 n﹣1 ①2S=12+3×22+…+(2n﹣3)×2 n﹣1+(2n﹣1)×2n ②
①﹣②得,﹣S=1×20+2(2+22+…+2 n﹣1)﹣(2n﹣1)2n,
化简得,S=(2n﹣1)2n﹣2 n+1+3,
故
 =n(2n﹣1)×2n﹣n×2 n+1+3n.
=n(2n﹣1)×2n﹣n×2 n+1+3n.
练习册系列答案
相关题目

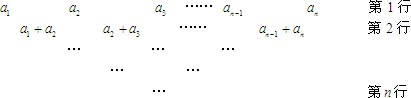
 .
.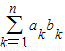 .
.