题目内容
某大学毕业生参加某单位的应聘考试,考核依次分为笔试,面试、实际操作共三轮进行,规定只有通过前一轮考核才能进入下一轮考核,否则被淘汰,三轮考核都通过才能被正式录用,设该大学毕业生通过一、二、三轮考核的概率分别为| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
①求该大学毕业生进入第三轮考核的概率;
②设该大学毕业生在应聘考核中考核轮数为X,求X的概率分布列及期望和方差.
分析:①根据所给的概率,利用相互独立事件的概率乘法公式即可做出结果.
②设该大学毕业生在应聘考核中考核轮数为X,X的次数的取值是1、2、3,根据互斥事件和相互独立事件同时发生的概率列出分布列,最后做出分布列和期望即可.
②设该大学毕业生在应聘考核中考核轮数为X,X的次数的取值是1、2、3,根据互斥事件和相互独立事件同时发生的概率列出分布列,最后做出分布列和期望即可.
解答:解:①记“该大学生通过第一轮考核”为事件A,“该大学生通过第二轮考核”为事件B,“该大学生通过第三轮考核”为事件C,则:P(A)=
P(B)=
P(C)=
…(2分)
那么该大学生进入第三轮考核的概率是P=P(A)•P(B)=
×
=
…(4分)
②
EX=1×
+2×
+3×
=
DX=(1-
)2×
+(2-
)2×
+(3-
)2×
=
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
那么该大学生进入第三轮考核的概率是P=P(A)•P(B)=
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
②
| X | 1 | 2 | 3 | ||||||
| P |
|
|
|
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 13 |
| 6 |
DX=(1-
| 13 |
| 6 |
| 1 |
| 3 |
| 13 |
| 6 |
| 1 |
| 6 |
| 13 |
| 6 |
| 1 |
| 2 |
| 29 |
| 36 |
点评:考查运用概率知识解决实际问题的能力,相互独立事件是指,两事件发生的概率互不影响,而对立事件是指同一次试验中,不会同时发生的事件,遇到求用至少来表述的事件的概率时,往往先求它的对立事件的概率.

练习册系列答案
相关题目
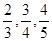 ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。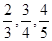 ,且各轮考核通过与否相互独立。
,且各轮考核通过与否相互独立。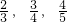 ,且各轮考核通过与否相互独立.
,且各轮考核通过与否相互独立.