题目内容
已知向量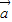 =(cosα,1),
=(cosα,1),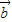 =(-2,sinα),
=(-2,sinα),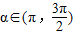 ,且
,且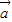 ⊥
⊥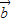
(1)求sinα的值;
(2)求
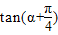 的值.
的值.
【答案】分析:(1)先根据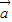 ⊥
⊥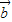 等价于
等价于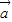 •
•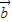 =0,得到角α正余弦之间的关系,再由同角三角函数的基本关系可求得sinα的值.
=0,得到角α正余弦之间的关系,再由同角三角函数的基本关系可求得sinα的值.
(2)先根据(1)中结果求出cosα的值,进而可得tanα的值,再由两角和与差的正切公式得到最好答案.
解答:解:(Ⅰ)由向量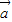 =(cosα,1),
=(cosα,1),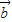 =(-2,sinα),
=(-2,sinα),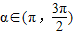 ,且
,且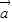 ⊥
⊥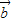 .
.
得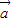 •
•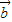 =(cosα,1)•(-2,sinα)=0.
=(cosα,1)•(-2,sinα)=0.
即-2cosα+sinα=0.
所以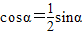 .
.
因为sin2α+cos2α=1,
所以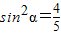 .
.
因为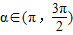 ,
,
所以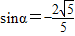 .
.
(Ⅱ)由(Ⅰ)可得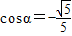 .
.
则tanα=2.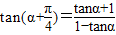 =-3.
=-3.
点评:本题主要考查向量的运算、同角三角函数的基本关系和两角和与差的正切公式.考查综合运用能力.
 ⊥
⊥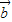 等价于
等价于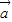 •
•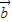 =0,得到角α正余弦之间的关系,再由同角三角函数的基本关系可求得sinα的值.
=0,得到角α正余弦之间的关系,再由同角三角函数的基本关系可求得sinα的值.(2)先根据(1)中结果求出cosα的值,进而可得tanα的值,再由两角和与差的正切公式得到最好答案.
解答:解:(Ⅰ)由向量
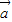 =(cosα,1),
=(cosα,1),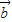 =(-2,sinα),
=(-2,sinα),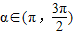 ,且
,且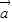 ⊥
⊥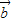 .
.得
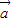 •
•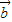 =(cosα,1)•(-2,sinα)=0.
=(cosα,1)•(-2,sinα)=0.即-2cosα+sinα=0.
所以
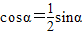 .
.因为sin2α+cos2α=1,
所以
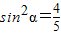 .
.因为
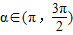 ,
,所以
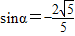 .
.(Ⅱ)由(Ⅰ)可得
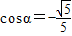 .
.则tanα=2.
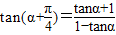 =-3.
=-3.点评:本题主要考查向量的运算、同角三角函数的基本关系和两角和与差的正切公式.考查综合运用能力.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |