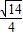Question

已知AD是边长为2的正三角形ABC的边上的高，沿AD将△ABC折成直二面角后，点A到BC的距离为（　　）

• A．

  3

  2

• B．

  7

  2

• C．

  14

  2

• D．

  14

  4

Answer 1

分析：确定∠BDC=90°，过D作DO垂直于BC于O，所以O是BC的中点，连接AO，证明AO即为点A到BC的距离，即可求出结论．

解答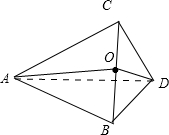：解：如图，因为AD是正△ABC的高线，所以∠BDC即为二面角的平面角，即∠BDC=90°，
过D作DO垂直于BC于O，所以O是BC的中点，连接AO．
因为CD=BD=1，所以BC=

2

，所以DO=

2

2

因为AD⊥底面BDC，所以AD⊥BC，
又因为DO⊥BC，并且AD∩DO=D，
所以BC⊥面ADO，所以BC⊥AO，即AO即为点A到BC的距离
∴A0=

3+ 1 2

=

14

2

故选C．

点评：本题考查面面角，考查空间距离的计算，属于中档题．