题目内容
设F1(-4,0)、F2(4,0)为定点,动点M满足|MF1|+|MF2|=8,则动点M的轨迹是( )
分析:首先确定点M在直线上,再利用长度关系,确定点M在线段F1F2上,从而得到结论.
解答:解:若点M与F1,F2可以构成一个三角形,则|MF1|+|MF2|>|F1F2|,
∵|F1F2|=8,动点M满足|MF1|+|MF2|=8,
∴点M在线段F1F2上.
故选D.
∵|F1F2|=8,动点M满足|MF1|+|MF2|=8,
∴点M在线段F1F2上.
故选D.
点评:本题考查轨迹的求法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
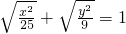 的曲线为C,关于曲线C有下列命题:
的曲线为C,关于曲线C有下列命题: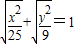 的曲线为C,关于曲线C有下列命题:
的曲线为C,关于曲线C有下列命题: