题目内容
在平面直角坐标系xOy中,设F1(-4,0),F2(4,0),方程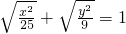 的曲线为C,关于曲线C有下列命题:
的曲线为C,关于曲线C有下列命题:
①曲线C是以F1、F2为焦点的椭圆的一部分;
②曲线C关于x轴、y轴、坐标原点O对称;
③若P是上任意一点,则PF1+PF2≤10;
④若P是上任意一点,则PF1+PF2≥10;
⑤曲线C围成图形的面积为30.
其中真命题的序号是________.
②③⑤
分析:先化简方程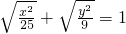 ,将根号去掉,判断出其表示的图形是四条线段,画出图形,判断出各命题的正误.
,将根号去掉,判断出其表示的图形是四条线段,画出图形,判断出各命题的正误.
解答:∵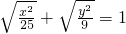 即为
即为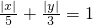 表示四条线段,如图
表示四条线段,如图

故①④错,②③对
对于⑤,图形的面积为 ,故⑤对.
,故⑤对.
故答案为②③⑤
点评:在判断曲线的性质时,常通过化简曲线的方程,通过研究方程判断出具有的性质.
分析:先化简方程
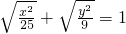 ,将根号去掉,判断出其表示的图形是四条线段,画出图形,判断出各命题的正误.
,将根号去掉,判断出其表示的图形是四条线段,画出图形,判断出各命题的正误.解答:∵
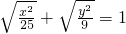 即为
即为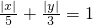 表示四条线段,如图
表示四条线段,如图
故①④错,②③对
对于⑤,图形的面积为
 ,故⑤对.
,故⑤对.故答案为②③⑤
点评:在判断曲线的性质时,常通过化简曲线的方程,通过研究方程判断出具有的性质.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
在平面直角坐标系xOy中,双曲线中心在原点,焦点在y轴上,一条渐近线方程为x-2y=0,则它的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.