题目内容
6．在平面直角坐标系xOy中，不等式组$\left\{\begin{array}{l}x+y-3≤0\\ x-y≥0\\ y≥0\end{array}\right.$表示的平面区域内坐标为整数的点的个数是（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 作出不等式组对应的平面区域，利用数形结合或者分类讨论进行求解即可．
解答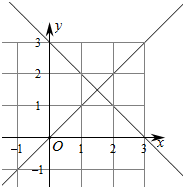 
解：作出不等式组对应的平面区域如图：
则区域内共有6个正数点，
法2．当y=0时，不等式组等价为$\left\{\begin{array}{l}{x≤3}\\{x≥0}\end{array}\right.$，即0≤x≤3，此时x=0，1，2，3，
．当y=1时，不等式组等价为$\left\{\begin{array}{l}{x≤2}\\{x≥1}\end{array}\right.$，即1≤x≤2，此时x=1，2，
．当y=2时，不等式组等价为$\left\{\begin{array}{l}{x≤1}\\{x≥2}\end{array}\right.$，此时不等式无解，
共有6个正数点，
故选：C．
点评 本题主要考查二元一次不等式组表示平面区域，利用数形结合或者分类讨论是解决本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目