题目内容
14.我国明朝著名数学家程大位在其名著《算法统宗》中记载了如下数学问题:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯”.诗中描述的这个宝塔古称浮屠,本题说它一共有7层,每层悬挂的红灯数是上一层的2倍,共有381盏灯,那么塔顶有( )盏灯.| A. | 2 | B. | 3 | C. | 5 | D. | 6 |
分析 设顶层有x盏灯根据题意得:x+2x+4x+8x+16x+32x+64x=381,由此能求出结果.
解答 解:设顶层有x盏灯
根据题意得:x+2x+4x+8x+16x+32x+64x=381
解得:x=3.
因此尖头(最顶层)有3盏灯.
故选:B.
点评 本题考查等比数列的首项的求法,是基础题,解题时要认真审,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
5.已知抛物线的方程为y2=2mx(m>0),焦点坐标为(1,0),则m等于( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
19.若sin(θ-$\frac{π}{6}$)=$\frac{1}{4}$,$θ∈({\frac{π}{6},\frac{2π}{3}})$,则$cos({\frac{3π}{2}+θ})$的值为( )
| A. | $\frac{{\sqrt{15}+\sqrt{3}}}{8}$ | B. | $\frac{{\sqrt{15}-\sqrt{3}}}{8}$ | C. | $\frac{{-\sqrt{15}+\sqrt{3}}}{8}$ | D. | $\frac{{-\sqrt{15}-\sqrt{3}}}{8}$ |
6.已知?ABCD的三个顶点的坐标分别是A(0,1),B(1,0),C(4,3),则顶点D的坐标为( )
| A. | (3,4) | B. | (4,3) | C. | (3,1) | D. | (3,8) |
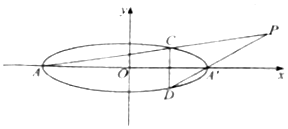 如图所示,椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左,右顶点分别为A,A′,线段CD是垂直于椭圆长轴的弦,连接AC,DA′相交于点P,则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1.
如图所示,椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左,右顶点分别为A,A′,线段CD是垂直于椭圆长轴的弦,连接AC,DA′相交于点P,则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1.