题目内容
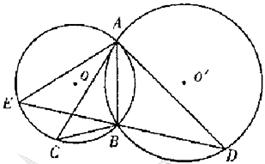
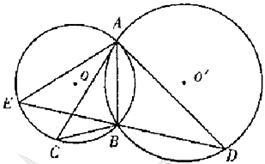
如图，⊙O和⊙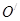
相交于A，B两点，过A作两圆的切线分别交两圆于C，D两点，连接DB并延长交⊙O于点E。证明：
(Ⅰ)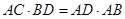
；
(Ⅱ) 
。
【答案】
见解析
【解析】证明：(Ⅰ)由AC与⊙
相切于A，得
，
同理
所以
∽
，
从而
,即
(Ⅱ)由AD与⊙相切于A，得
,
又
得
∽
,
从而
即
.
结合(Ⅰ)的结论，AC=AE.
考点定位：本大题主要以圆为几何背景考查线线相等的证明及相似三角形的证明，可以运用直线与圆相切的性质证角相等，运用相似三角形的基本证明方法求证.
练习册系列答案
相关题目
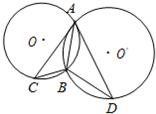如图圆O和圆O′相交于A，B两点，AC是圆O′的切线，AD是圆O的切线，若BC=2，AB=4，求BD．
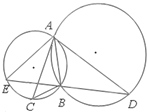选修4-1几何证明选讲
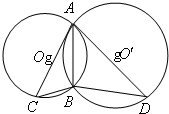（2010•广东模拟）（几何证明选讲）如图，⊙O和⊙O'相交于A，B两点，AC是⊙O'的切线，交⊙O于点C，AD是⊙O的切线，交⊙O'于点D，若BC=2，BD=8，则AB=
相交于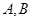
两点，过A作两圆的切线分别交两圆于C，D两点，连接DB并延长交⊙O于点E。证明
；
。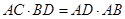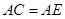