题目内容

选修4-1几何证明选讲
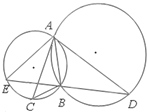
如图，⊙O和⊙O′相交于A，B两点，过A作两圆的切线分别交两圆于C，D两点，连接DB并延长交⊙O于点E．证明：AC•BD=AD•AB．
分析：利用圆的切线的性质得∠CAB=∠ADB，∠ACB=∠DAB，从而有△ACB∽△DAB，进而得到结论；
解答：证明：（I）∵AC与⊙O'相切于点A，故∠CAB=∠ADB，
同理可得∠ACB=∠DAB，
∴△ACB∽△DAB，∴
AC
AD
=
AB
BD
，
∴AC•BD=AD•AB．
点评：本题主要考查圆的切线的性质，利用两个三角形相似得到成比列线段，是解题的关键，属于中档题．
练习册系列答案
相关题目
精英家教网A．（选修4-4坐标系与参数方程）已知点A是曲线ρ=2sinθ上任意一点，则点A到直线ρsin(θ+
π3
)=4的距离的最小值是
 
．
B．（选修4-5不等式选讲）不等式|x-log2x|＜x+|log2x|的解集是
 
．
C．（选修4-1几何证明选讲）如图所示，AC和AB分别是圆O的切线，且OC=3，AB=4，延长AO到D点，则△ABD的面积是
 
．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
A．（不等式选做题）不等式|2x-1|＜3的解集为
（-1，2）
（-1，2）
．
B、（选修4-1几何证明选讲） 如图所示，AC和AB分别是⊙O的切线，且OC=3，AB=4，延长AO到D点，则△ABC的面积是
192
25
192
25
．
C．（坐标系与参数方程选做题）参数方程
x=cosα
y=1+sinα
（α为参数）化成普通方程为
x2+（y-1）2=1
x2+（y-1）2=1
．
（选修4-1几何证明选讲）
如图，D，E分别是AB，AC边上的点，且不与顶点重合，已知AE=m，AC=n，AD，AB为方程x2-14x+mn=0的两根
（1）证明：C，B，D，E四点共圆；
（2）若∠A=90°，m=4，n=6，求C，B，D，E四点所在圆的半径．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（选修4-5 不等式选讲）
若任意实数x使m≥|x+2|-|5-x|恒成立，则实数m的取值范围是
[7，+∞）
[7，+∞）
；
B．（选修4-1 几何证明选讲）
如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的度数是
99°
99°
；
C．（选修4-4坐标系与参数方程）
极坐标系下，直线ρcos(θ-
π
4
)=
2
与圆ρ=
2
的公共点个数是
1
1
．
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
（A）（选修4-4坐标系与参数方程）已知点A是曲线ρ=2sinθ上任意一点，则点A到直线ρsin(θ+
π
3
)=4的距离的最小值是
5
2
5
2
．
（B）（选修4-5不等式选讲）已知2x+y=1，x＞0，y＞0，则
x+2y
xy
的最小值是
9
9
．
（C）（选修4-1几何证明选讲）若直角△ABC的内切圆与斜边AB相切于点D，且AD=1，BD=2，则△ABC的面积为
2
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网