题目内容
已知函数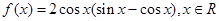 .
.
(Ⅰ)求函数 图像的对称中心;
图像的对称中心;
(Ⅱ)求函数 在区间
在区间 上的最小值和最大值.
上的最小值和最大值.
(Ⅰ) ,
, ;(Ⅱ)最大值为
;(Ⅱ)最大值为 ,最小值为-2.
,最小值为-2.
解析试题分析:(Ⅰ) 通过三角恒等变换化简函数,然后利用 图形来求;(Ⅱ)分析函数的单调性,然后求最值.
图形来求;(Ⅱ)分析函数的单调性,然后求最值.
试题解析:(I)
因此,函数 图象的对称中心为
图象的对称中心为 ,
, .
.
(Ⅱ)因为 在区间
在区间 上为增函数,在区间
上为增函数,在区间 上为减函数,
上为减函数,
又 ,
, ,
,
故函数 在区间
在区间 上的最大值为
上的最大值为 ,最小值为-2.
,最小值为-2.
考点:三角恒等变换、函数图象与性质,考查分析问题、解决问题的能力.

练习册系列答案
相关题目
 ,若
,若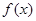 的最大值为1
的最大值为1 的值,并求
的值,并求 中,角
中,角 、
、 、
、 的对边
的对边 、
、 、
、 ,若
,若 ,且
,且 ,试判断三角形的形状.
,试判断三角形的形状. ,
, ,且
,且 ,其中A、B、C是
,其中A、B、C是 ABC的内角,
ABC的内角, 分别是角A,B,C的对边。
分别是角A,B,C的对边。 的取值范围;
的取值范围; 的图象过点(0,
的图象过点(0,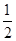 ),最小正周期为
),最小正周期为 ,且最小值为-1.
,且最小值为-1. 的解析式.
的解析式. ,
, ,求m的取值范围.
,求m的取值范围.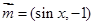 ,向量
,向量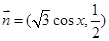 ,函数
,函数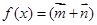 ·
·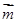 .
. 的最小正周期T;
的最小正周期T;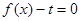 在
在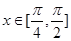 上有解,求实数
上有解,求实数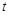 的取值范围.
的取值范围. ,中心角
,中心角 .求证:当
.求证:当 时该扇形面积最大;
时该扇形面积最大;
 .求证:
.求证: .
.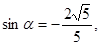 且
且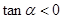
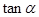 的值;
的值;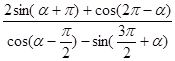 的值;
的值;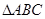 中,角
中,角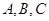 所对的边分别为
所对的边分别为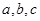 ,且
,且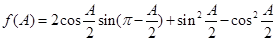 .
.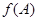 的最大值;
的最大值;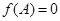 ,
,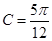 ,
,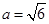 ,求
,求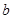 的值.
的值.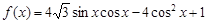 .
.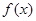 在
在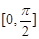 上的值域;
上的值域;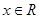 ,不等式
,不等式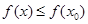 恒成立,求
恒成立,求 .
.