题目内容
等差数列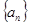 和
和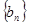 的前
的前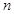 项和分别为
项和分别为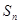 和
和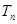 ,且
,且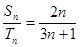 ,则
,则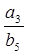 =( )
=( )
A.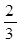 | B.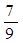 | C.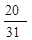 | D.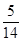 |
D
解析试题分析:本题容易由等差数列的性质,联想等差数列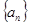 的前
的前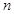 项和
项和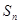 与项
与项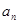 之间的关系:
之间的关系: ,所以我们有
,所以我们有 ,即
,即 ,当然
,当然 不可能直接利用已知条件
不可能直接利用已知条件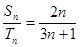 ,考虑到等差数列的前
,考虑到等差数列的前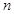 项和
项和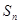 一定为
一定为 这种形式,故我们可以得出
这种形式,故我们可以得出 ,从而可设
,从而可设 ,(
,( 为常数)的形式,于是有:
为常数)的形式,于是有: .选D.
.选D.
考点:等差数列的前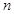 项和.
项和.

练习册系列答案
相关题目
已知等差数列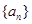 的公差为2,若
的公差为2,若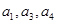 成等比数列,则a2=( )
成等比数列,则a2=( )
| A.-4 | B.-6 | C.-8 | D.-10 |
等差数列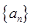 公差为2,若
公差为2,若 ,
,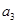 ,
, 成等比数列,则
成等比数列,则 等于( )
等于( )
| A.-4 | B.-6 | C.-8 | D.-10 |
已知等差数列 中,
中, ,记数列
,记数列 的前
的前 项和为
项和为 ,若
,若 ,对任意的
,对任意的 成立,则整数
成立,则整数 的最小值为( )
的最小值为( )
| A.5 | B.4 | C.3 | D.2 |
已知数列 是等差数列,且
是等差数列,且 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知数列 为等比数列,且
为等比数列,且 ,设等差数列
,设等差数列 的前n项和为
的前n项和为 ,若
,若 ,则
,则 =( )
=( )
| A.36 | B.32 | C.24 | D.22 |
在等差数列 中,
中, ,前n项的和是
,前n项的和是 ,则使
,则使 最大的项是( )
最大的项是( )
| A.第5项 | B.第6项 |
| C.第5项或第6项 | D.第6项或第7项 |
设 是等差数列
是等差数列 的前
的前 项和,
项和, ,则
,则 ( )
( )
A. | B. | C. | D. |
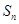 为等差数列
为等差数列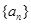 的前
的前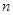 项和,
项和, ,
, ,正项等比数列
,正项等比数列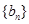 中,
中, ,
, ,则
,则 =( )
=( )
| A.8 | B.9 | C.10 | D.11 |