题目内容
设 是等差数列
是等差数列 的前
的前 项和,
项和, ,则
,则 ( )
( )
A. | B. | C. | D. |
B
解析试题分析: 得
得 ,即
,即 ,所以
,所以 ,选B.
,选B.
考点:1.等差数列的通项公式;2.等差数列的求和公式.

练习册系列答案
相关题目
已知数列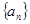 是等差数列,且
是等差数列,且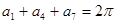 ,则
,则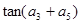 的值为( )
的值为( )
A.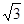 | B.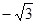 | C.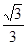 | D.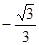 |
等差数列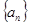 和
和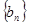 的前
的前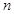 项和分别为
项和分别为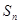 和
和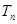 ,且
,且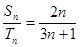 ,则
,则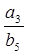 =( )
=( )
A.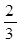 | B.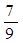 | C.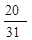 | D.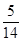 |
已知数列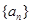 的前
的前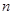 项和
项和 ,则
,则 ( )
( )
A. | B. | C. | D. |
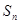 为等差数列
为等差数列 的前
的前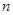 项和,
项和, ,则
,则 ( )
( )
A. | B. | C. | D. |
在等差数列 等于( )
等于( )
| A.9 | B.27 | C.18 | D.54 |
.等差数列 满足
满足 则
则 ( )
( )
| A.17 | B.18 | C.19 | D.20 |
等差数列 中,已知
中,已知 ,
, ,使得
,使得 的最小正整数n为 ( )
的最小正整数n为 ( )
| A.7 | B.8 | C.9 | D.10 |
等差数列 中的
中的 、
、 是函数
是函数 的极值点,则
的极值点,则 ( )
( )
A. | B. | C. | D. |