题目内容

证明：
sin2x
2cosx
(1+tanx•tan
x
2
)=tanx．
分析：从左到由，利用二倍角公式，同角的商数关系，即可证得结论．
解答：证明：∵
sin2x
2cosx
(1+tanx•tan
x
2
)=
2sinxcosx
2cosx
(1+tanx•tan
x
2
)=sinx(1+tanx•tan
x
2
)
=sinx（1+
2sin
x
2
cos
x
2
cosx
•
sin
x
2
cos
x
2
）=sinx（1+
1-cosx
cosx
）=tanx
∴
sin2x
2cosx
(1+tanx•tan
x
2
)=tanx
点评：本题考查三角恒等式的证明，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知a，b，c∈R，证明不等式：a6+8b6+
127
c6≥2a2b2c2．
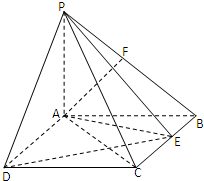精英家教网如图，PA⊥平面ABCD，四边形ABCD是矩形，PA=AB=1，PD与平面ABCD所成角是30°，点F是PB的中点，点E在矩形ABCD的边BC上移动．
（Ⅰ）证明：无论点E在边BC的何处，都有PE⊥AF；
（Ⅱ）当CE等于何值时，二面角P-DE-A的大小为45°．
设点An（xn，0），Pn（xn，2n-1）和抛物线Cn：y=x2+anx+bn（n∈N*），其中an=-2-4n-
12n-1
，xn由以下方法得到：x1=1，点P2（x2，2）在抛物线C1：y=x2+a1x+b1上，点A1（x1，0）到P2的距离是A1到C1上点的最短距离，…，点Pn+1（xn+1，2n）在抛物线Cn：y=x2+anx+bn上，点An（xn，0）到Pn+1的距离是An到Cn上点的最短距离．
（Ⅰ）求x2及C1的方程．
（Ⅱ）证明{xn}是等差数列．
A是由在[1，4]上有意义且满足如下条件的函数φ（x）组成的集合；
①对任意x∈[1，2]，都有φ（2x）∈（1，2）；
②存在常数L（0＜L＜1），使得对任意的x1，x2∈[1，2]都有|φ（2x1）-φ（2x2）|=L|x1-x2|
（1）设φ(x)=
2x+15
18
，x∈[1，2]，证明：φ（x）∈A；
（2）设φ(x)=
x2+15
18
，x∈[1，2]，是否存在设x0∈（1，2），使得x0=φ（2x0），如存在，求出所有的x0，如不存在请说明理由！
已知函数f（x）=-x2+2x
（1）证明函数f（x）在（-∞，1]上是增函数；
（2）当x∈[-5，-2]时，f（x）是增函数还是减函数？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网