题目内容
一只蚂蚁在边长为4的正三角形内爬行,某时刻此蚂蚁距三角形三个顶点的距离均超过1的概率为( )A.1-
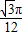
B.1-
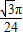
C.
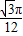
D.
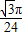
【答案】分析:根据题意,记“蚂蚁距三角形三个顶点的距离均超过1”为事件A,则其对立事件 为“蚂蚁与三角形的三个顶点的距离不超过1”,先求得边长为4的等边三角形的面积,再计算事件
为“蚂蚁与三角形的三个顶点的距离不超过1”,先求得边长为4的等边三角形的面积,再计算事件 构成的区域面积,由几何概型可得P(
构成的区域面积,由几何概型可得P( ),进而由对立事件的概率性质,可得答案.
),进而由对立事件的概率性质,可得答案.
解答:解:记“蚂蚁距三角形三个顶点的距离均超过1”为事件A,则其对立事件 为“蚂蚁与三角形的三个顶点的距离不超过1”,
为“蚂蚁与三角形的三个顶点的距离不超过1”,
边长为4的等边三角形的面积为S= ×42=4
×42=4 ,
,
则事件 构成的区域面积为S(
构成的区域面积为S( )=3×
)=3×


 π×12=
π×12= ,
,
由几何概型的概率公式得P( )=
)= =
= ;
;
P(A)=1-P( )=1-
)=1- ;
;
故选B.
点评:本题考查几何概型,涉及对立事件的概率性质;解题时如需要计算不规则图形的面积,可用间接法.
 为“蚂蚁与三角形的三个顶点的距离不超过1”,先求得边长为4的等边三角形的面积,再计算事件
为“蚂蚁与三角形的三个顶点的距离不超过1”,先求得边长为4的等边三角形的面积,再计算事件 构成的区域面积,由几何概型可得P(
构成的区域面积,由几何概型可得P( ),进而由对立事件的概率性质,可得答案.
),进而由对立事件的概率性质,可得答案.解答:解:记“蚂蚁距三角形三个顶点的距离均超过1”为事件A,则其对立事件
 为“蚂蚁与三角形的三个顶点的距离不超过1”,
为“蚂蚁与三角形的三个顶点的距离不超过1”,边长为4的等边三角形的面积为S=
 ×42=4
×42=4 ,
,则事件
 构成的区域面积为S(
构成的区域面积为S( )=3×
)=3×


 π×12=
π×12= ,
,由几何概型的概率公式得P(
 )=
)= =
= ;
;P(A)=1-P(
 )=1-
)=1- ;
;故选B.
点评:本题考查几何概型,涉及对立事件的概率性质;解题时如需要计算不规则图形的面积,可用间接法.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 B.
B.  C.
C. D.
D.



