题目内容
已知△ABC的面积为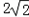 ,内角A,B,C的对边分别为a,b,c,已知a=3,b=4,0<C<90°.
,内角A,B,C的对边分别为a,b,c,已知a=3,b=4,0<C<90°.
(1)求sin(A+B)的值;
(2)求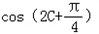 的值;
的值;
(3)求向量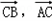 的数量积
的数量积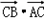 .
.
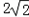 ,内角A,B,C的对边分别为a,b,c,已知a=3,b=4,0<C<90°.
,内角A,B,C的对边分别为a,b,c,已知a=3,b=4,0<C<90°.(1)求sin(A+B)的值;
(2)求
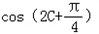 的值;
的值;(3)求向量
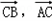 的数量积
的数量积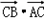 .
.解:(1)由 absinC=2
absinC=2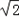 ,即
,即 ×3×4sinC=2
×3×4sinC=2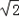 ,得sinC=
,得sinC=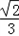 .
.
∵A+B=180°﹣C,
∴sin(A+B)=sin(180°﹣C)=sinC=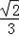
(2)由(1)得sinC=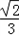 ,
,
∵0<C<90°,
∴cosC=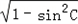 =
=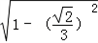 =
=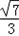
∴cos2C=2cos2C﹣1=2×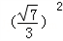 ﹣1=
﹣1= .
.
∴sin2C=2sinCcosC=2×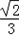 ×
×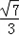 =
=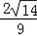
∴cos(2C+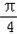 )=cos2Ccos
)=cos2Ccos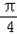 ﹣sin2Csin
﹣sin2Csin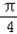 =
= ×
×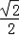 ﹣
﹣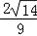 ×
×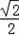 =﹣
=﹣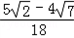 .
.
(3)∵|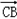 |=a=3,
|=a=3,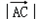 =b=4,
=b=4,
设向量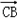 与
与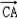 所成的角为θ,则θ=180°﹣C
所成的角为θ,则θ=180°﹣C
∴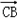

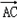 =
=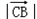
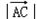 cosθ=abcos(180°﹣C)=﹣abcosC=﹣3×4×
cosθ=abcos(180°﹣C)=﹣abcosC=﹣3×4×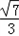 =﹣4
=﹣4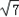

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使 (2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.
(2012•温州一模)如图,在△ABC中,AD⊥BC,垂足为D,且BD:DC:AD=2:3:6.