题目内容
已知曲线y=2sinx与曲线y=ax2+bx+
的一个交点P的横坐标为
,且两曲线在交点P处的切线与两坐标轴围成的四边形恰好有外接圆,则a与b的值分别为( )
| 3 |
| 2π |
| 3 |
A.a=
| B.a=
| C.a=-
| D.a=
|
因为点P横坐标
,
点P在y=2sinx上,因此点P坐标是(
,
);
点P在y=ax2+bx+
上,因此有
a+b=0①
y=2sinx在点P处的切线的斜率为2cos
=-1,
因为两切线与两坐标轴围成的四边形恰有外接圆,且P点在第一象限.
因此两切线垂直(有外接圆的四边形对角和为180度).即两切线斜率乘积为-1.
因此,y=ax2+bx+
在点P处的斜率为1.
又y′=2ax+b可以得出其在点P处的斜率为2a×
+b=1 ②.
由①②得:
.
故选:D.
| 2π |
| 3 |
点P在y=2sinx上,因此点P坐标是(
| 2π |
| 3 |
| 3 |
点P在y=ax2+bx+
| 3 |
| 2π |
| 3 |
y=2sinx在点P处的切线的斜率为2cos
| 2π |
| 3 |
因为两切线与两坐标轴围成的四边形恰有外接圆,且P点在第一象限.
因此两切线垂直(有外接圆的四边形对角和为180度).即两切线斜率乘积为-1.
因此,y=ax2+bx+
| 3 |
又y′=2ax+b可以得出其在点P处的斜率为2a×
| 2π |
| 3 |
由①②得:
|
故选:D.

练习册系列答案
相关题目
 )cos(
)cos(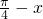 )与直线y=
)与直线y= 相交,若在y轴右侧的交点自左向右依次记为P1,P2,P3,…,则|
相交,若在y轴右侧的交点自左向右依次记为P1,P2,P3,…,则|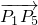 |等于
|等于