题目内容
已知函数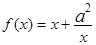 ,
,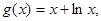 其中
其中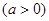
(Ⅰ)若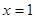 是函数
是函数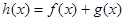 的极值点,求实数
的极值点,求实数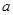 的值;
的值;
(Ⅱ)若对任意的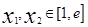 (
(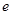 为自然对数的底数)都有
为自然对数的底数)都有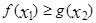 成立,求实数
成立,求实数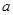 的取值范围
的取值范围
(Ⅰ)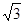 ;(Ⅱ)
;(Ⅱ)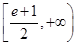 .
.
【解析】
试题分析:(Ⅰ)若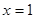 是函数
是函数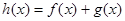 的极值点,求实数
的极值点,求实数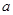 的值,先函数
的值,先函数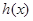 的定义域,与极值有关,可通过求导解决.对
的定义域,与极值有关,可通过求导解决.对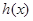 求导,由题意可知
求导,由题意可知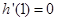 ,可求出
,可求出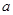 的值;(Ⅱ)若对任意的
的值;(Ⅱ)若对任意的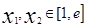 都有
都有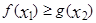 成立,即
成立,即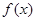 在
在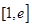 上的最小值大于或等于
上的最小值大于或等于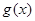 在
在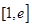 上的最大值,从而转化为分别求函数
上的最大值,从而转化为分别求函数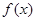 ,
,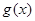 在
在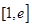 的最小值、最大值,由它们的最值,从而确定出实数
的最小值、最大值,由它们的最值,从而确定出实数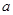 的取值范围.
的取值范围.
试题解析:(I)解法1:∵h(x)=2x+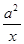 +lnx,其定义域为(0,+∞), (1分)
+lnx,其定义域为(0,+∞), (1分)
∴h'`(x)=2-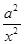 -
-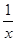 (3分)
(3分)
∵x=1是函数h(x)的极值点,∴h'(1)=0,即3-a2=0.∵a>0,∴a=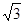 .
.
经检验当a=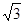 时,x=1是函数h(x)的极值点,∴a=
时,x=1是函数h(x)的极值点,∴a=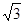 . (5分)
. (5分)
解法2:∵h(x)=2x+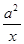 +lnx,其定义域为(0,+∞),
+lnx,其定义域为(0,+∞),
∴h'`(x)=2-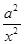 -
-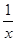 . 令h`(x)=0,即2-
. 令h`(x)=0,即2-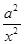 -
-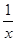 =0,整理,得2x2+x-a=0.
=0,整理,得2x2+x-a=0.
∵D=1+8a2>0,
∴h`(x)=0的两个实根x1=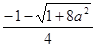 (舍去),x2=
(舍去),x2=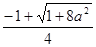 ,
,
当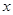 变化时,h(x),h`(x)的变化情况如下表:
变化时,h(x),h`(x)的变化情况如下表:
|
x |
(0,x2) |
|
(x2,+∞) |
|
h`(x) |
- |
0 |
+ |
|
h(x) |
↘ |
极小值 |
↗ |
依题意,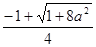 =1,即a2=3,∵a>0,∴a=
=1,即a2=3,∵a>0,∴a=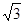 .
.
(Ⅱ)对任意的x1,x2∈[1,e]都有f(x1)≥g(x2)成立等价于对任意的x1,x2∈[1,e]都有[f(x)]min≥[g(x)]max
(6分)
当x∈[1,e]时,g`(x)=1+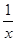 >0.
>0.
∴函数g(x)=x+lnx在[1,e]上是增函数.∴[g(x)]max=g(e)=e+1. (8分)
∵f'`(x)=1-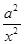 =
=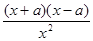 ,且x∈[1,e],a>0.
,且x∈[1,e],a>0.
①当0<a<1且x∈[1,e]时,f`(x)>0,
∴函数f(x)=x+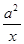 在[1,e]上是增函数,
在[1,e]上是增函数,
∴[f(x)]min=f(1)=1+a2,由1+a2≥e+1,得a≥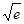 ,又∵0<a<1,
,又∵0<a<1,
∴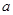 不合题意. (10分)
不合题意. (10分)
②当1≤a≤e时,
若1≤x<a,则f'`(x)=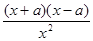 <0;若a<x≤e,则f`(x)=
<0;若a<x≤e,则f`(x)=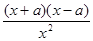 >0.
>0.
∴函数f(x)=x+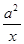 在[1,a]上是减函数,在(a,e]上是增函数.
在[1,a]上是减函数,在(a,e]上是增函数.
∴[f(x)]min=f(a)=2a.
由2a≥e+1,得a≥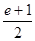 ,又1≤a≤e,∴
,又1≤a≤e,∴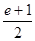 ≤a≤e. (12分)
≤a≤e. (12分)
③当a>e且x∈[1,e]时,f'(x)=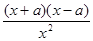 <0,
<0,
∴函数f(x)=x+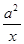 在[1,e]上是减函数.
在[1,e]上是减函数.
∴[f(x)]min=f(e)=e+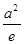 ,由e+
,由e+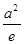 ≥e+1,得a≥
≥e+1,得a≥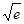 , (13分)
, (13分)
综上所述,a的取值范围为[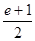 ,+∞) (14分)
,+∞) (14分)
考点:函数在某点取得极值的条件;函数恒成立问题.

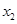






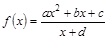 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.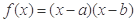 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
