题目内容
已知P(t,t),t∈R,点M是圆x2+(y-1)2=
上的动点,点N是圆(x-2)2+y2=
上的动点,则|PN|-|PM|的最大值是
| 1 |
| 4 |
| 1 |
| 4 |
2
2
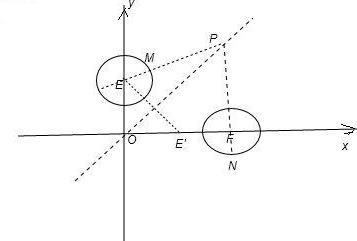
.分析:先根据两圆的方程求出圆心和半径,结合图形,把求|PN||-|PM|的最大值转化为|PF|-|PE|+1的最大值,再利用|PF|-|PE|=|PF|-|PE′|≤|E′F|=1,求出所求式子的最大值.
解答:解:如图:
圆 x2+(y-1)2=
的圆心E(0,1),圆 (x-2)2+y2=
的圆心 F(2,0),这两个圆的半径都是
.
要使|PN||-|PM|最大,需|PN|最大,且|PM|最小,由图可得,|PN|最大值为|PF|+
,PM|的最小值为|PE|-
,
故|PN||-|PM|最大值是 (|PF|+
)-(|PE|-
)=|PF|-|PE|+1,
点P(t,t)在直线 y=x上,E(0,1)关于y=x的对称点E′(1,0),直线FE′与y=x的交点为原点O,
则|PF|-|PE|=|PF|-|PE′|≤|E′F|=1,故|PF|-|PE|+1的最大值为1+1=2,
故答案为2.

圆 x2+(y-1)2=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
要使|PN||-|PM|最大,需|PN|最大,且|PM|最小,由图可得,|PN|最大值为|PF|+
| 1 |
| 2 |
| 1 |
| 2 |
故|PN||-|PM|最大值是 (|PF|+
| 1 |
| 2 |
| 1 |
| 2 |
点P(t,t)在直线 y=x上,E(0,1)关于y=x的对称点E′(1,0),直线FE′与y=x的交点为原点O,
则|PF|-|PE|=|PF|-|PE′|≤|E′F|=1,故|PF|-|PE|+1的最大值为1+1=2,
故答案为2.
点评:本题的考点是圆的方程的综合应用,主要考查圆的标准方程,点与圆的位置关系,体现了转化及数形结合的数学思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 上的动点,点N是圆
上的动点,点N是圆 上的动点,则|PN|-|PM|的最大值是________.
上的动点,则|PN|-|PM|的最大值是________. 上的动点,点N是圆
上的动点,点N是圆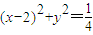 上的动点,则|PN|-|PM|的最大值是 .
上的动点,则|PN|-|PM|的最大值是 . 上的动点,点N是圆
上的动点,点N是圆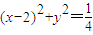 上的动点,则|PN|-|PM|的最大值是 .
上的动点,则|PN|-|PM|的最大值是 .