Question

在平面直角坐标系中，点为动点，分别为椭圆的左右焦点．已知△为等腰三角形．

（Ⅰ）求椭圆的离心率；

（Ⅱ）设直线与椭圆相交于两点，是直线上的点，满足，求点的轨迹方程．

Answer 1

本小题主要考查椭圆的标准方程和几何性质、直线的方程、平面向量等基础知识，考查用代数方法研究圆锥曲线的性质及数形结合的数学思想，考查解决问题能力与运算能力.满分13分.

   （I）解：设

    由题意，可得

即

整理得（舍），

或所以

（II）解：由（I）知

可得椭圆方程为

直线PF₂方程为

A，B两点的坐标满足方程组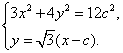

消去y并整理，得

解得

    得方程组的解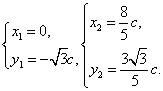

不妨设

设点M的坐标为，

由

于是

由

即，

化简得

将

所以

因此，点M的轨迹方程是