[题目]选修4-1:几何证明选讲如图.圆O的直径AB=10.P是AB延长线上一点.BP=2.割线PCD交圆O于点C.D.过点P作AP的垂线.交直线AC于点E.交直线AD于点F.(1)当时.求的度数,(2)求的值. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】选修4-1：几何证明选讲

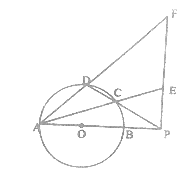
如图，圆O的直径AB=10，P是AB延长线上一点，BP=2，割线PCD交圆O于点C，D，过点P作AP的垂线，交直线AC于点E，交直线AD于点F.

（1）当时，求的度数；

（2）求的值.

【答案】（1）；（2）24.

【解析】

试题分析：（1）连接,可知,从而得到,进一步得到的值；

（2）由（1）可知,所以点四点共圆，那么.

试题解析：（1）连接BC，∵AB是圆O的直径，∴ACB=90°，

又APF=90°，CAB+CBA=EAP+PEC，

∴CBA=PEC，∵PEC=60°，∴PDF=CBA=PEC=60°.

（2）由（1）知PDF=PEC，

∴D、C、E、F四点共圆，∴，

∵PC、PA都是圆O的割线，∴，∴.

练习册系列答案

（1）求图中的值；

（2）设该市有500万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由：

（3）估计本市居民的月用水量平均数（同一组中的数据用该区间的中点值代表）.

【题目】某学校随机抽取20个班，调查各班中有网上购物经历的人数，所得数据的茎叶图如图所示．以组距为5将数据分组成[0，5)，[5，10)，…，[30，35)，[35，40]时，所作的频率分布直方图是( )

【题目】某班主任对全班50名学生进行了作业量多少的调查．数据如下表：

	认为作业多	认为作业不多	合计
喜欢玩游戏	18	9
不喜欢玩游戏	8	15
合计

（1）请完善上表中所缺的有关数据；

（2）试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少有关系？

附：

P（K2≥K0）	0.05	0.025	0.010	0.005	0.001
K0	3.841	5.024	6.635	7.879	10.828

【题目】已知函数（）．

（1）当时，判断在的单调性，并用定义证明．

（2）若对任意，不等式恒成立，求的取值范围；

（3）讨论的零点个数．

【题目】根据下列算法语句，当输入x为60时，输出y的值为

INPUT x

IF x<=50 THEN

y=0.5*x

ELSE

y=25+0.6*(x–50)

END IF

PRINT y

END

A. 25 B. 30 C. 31 D. 61

【题目】微信是腾讯公司推出的一种手机通讯软件，它支持发送语音短信、视频、图片和文字，一经推出便风靡全国，甚至涌现出一批在微信的朋友圈内销售商品的人（被称为微商）.为了调查每天微信用户使用微信的时间，某经销化妆品的微商在一广场随机采访男性、女性用户各50名，其中每天玩微信超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如下：

（1）根据以上数据，能否有60%的把握认为“微信控”与”性别“有关？

（2）现从调查的女性用户中按分层抽样的方法选出5人，从这5人中再随机抽取3人赠送200元的护肤品套装，求这3人中“微信控”的人数为2的概率.

参考公式：，其中n=a+b+c+d.

参考数据：

【题目】已知向量，，，且，，分别为△的三边所对的角．

（Ⅰ）求角的大小；

（Ⅱ）若，，成等比数列，且，求边C的值．

【题目】在平行四边形中，，点是线段的中点线段与交于点．

（1）求直线的方程；

（2）求点的坐标．

试题分类