题目内容
(本题满分15分)在平面直角坐标系![]() 中,过定点
中,过定点![]() 作直线
作直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(I)设![]() ,求
,求![]() 的最小值;
的最小值;
(II)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
解:(I)依题意,可设![]() ,
, ![]() ,直线AB的方程为:
,直线AB的方程为: ![]()
由![]()
![]() …………………2分
…………………2分
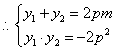
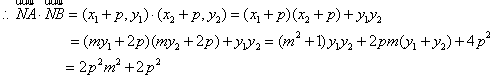
当m=0时![]() 的最小值为
的最小值为![]() .…………………7分
.…………………7分
(II)假设满足条件的直线![]() 存在,其方程为x=a,AC的中点为
存在,其方程为x=a,AC的中点为![]() ,
,![]() 与以AC为直径的圆
与以AC为直径的圆
相交于P,Q,PQ中点为H,则![]() ,
,![]() 的坐标为
的坐标为![]() .
.
![]() …………………9分
…………………9分
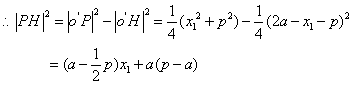
![]() …………………13分
…………………13分
令![]() =0得
=0得![]() .此时
.此时![]() 为定值.故满足条件的直线
为定值.故满足条件的直线![]() 存在,
存在,
其方程为x= ![]() …………………15分
…………………15分

练习册系列答案
相关题目
 的两个焦点为
的两个焦点为 ,椭圆的离心率为
,椭圆的离心率为 ,
,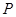 点是椭圆上任意一点, 且
点是椭圆上任意一点, 且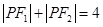 ,
,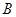 为直角顶点作椭圆的内接等腰直角三角形
为直角顶点作椭圆的内接等腰直角三角形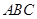 ,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.
,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.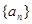 中,
中,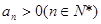 ,公比
,公比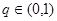 ,且
,且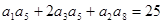 ,
,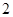 是
是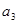 与
与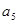 的等比中项。设
的等比中项。设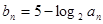 .
.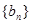 的通项公式;
的通项公式;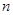 项和为
项和为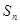 ,
,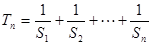 ,求
,求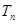 .
. 
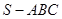 中,
中,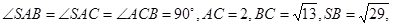
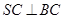 ;
;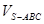


 的值。
的值。