题目内容
(本小题12分)
如图,四棱锥 中,底面ABCD为矩形,
中,底面ABCD为矩形, 底面ABCD,AD=PD=1,AB=
底面ABCD,AD=PD=1,AB= (
( ),E,F分别CD.PB的中点。
),E,F分别CD.PB的中点。
(Ⅰ)求证:EF 平面PAB;,
平面PAB;,
(Ⅱ)当 时,求AC与平面AEF所成角的正弦值。
时,求AC与平面AEF所成角的正弦值。
解: (Ⅰ)证明:建立如图所示的空间直角坐标系 (如图),---1分
(如图),---1分
AD=1,PD=1,AB=
 (
( ),则E(a,0,0), C(2a,0,0), A(0,1,0), B(2a,1,0), P(0,0,1),
),则E(a,0,0), C(2a,0,0), A(0,1,0), B(2a,1,0), P(0,0,1),  .得
.得 ,
, ,
,  。--------2分
。--------2分
由 ,得
,得 ,即
,即  ,--------4分
,--------4分
同理 ,又
,又 , ---------5分
, ---------5分
所 以,EF
以,EF 平面PAB。--
平面PAB。-- --------------6分
--------------6分
(Ⅱ)解:由 ,得
,得 ,
,
 ,
, 。
。
有 ,
, ,
,  。---------------7分
。---------------7分
设平面AEF的法向量为 ,由
,由

 ,解得
,解得 。于是
。于是 。----------------9分
。----------------9分
设AC与面AEF所成的角为 ,
, 与
与 的夹角为
的夹角为 。
。
则 。----------11分
。----------11分
所以,AC与平面AEF所成角的大小的正弦值为 -----------12分
-----------12分
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,AC=BC, AC⊥BC,点D是A1B1中点.
中,AC=BC, AC⊥BC,点D是A1B1中点.  ,求二面角D- AC1-A1的余弦值.
,求二面角D- AC1-A1的余弦值.
 中,
中, 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面 是
是 的菱形,
的菱形, 为
为 的中点.
的中点. 与底面
与底面 平面
平面 ;
; 的余弦值.
的余弦值. 
 中,底面
中,底面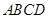 是正方形,
是正方形, ,
,  底面
底面 分别在
分别在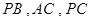 上,且
上,且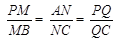
 ∥平面
∥平面 .
. 与平面面
与平面面
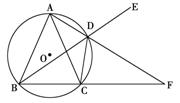

 平面BCD;
平面BCD;