题目内容
直线y=x与椭圆 =1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )A.

B.

C.

D.

【答案】分析:根据直线y=x与椭圆 =1的交点在x轴上的射影恰好是椭圆的焦点,可得(c,c)满足椭圆
=1的交点在x轴上的射影恰好是椭圆的焦点,可得(c,c)满足椭圆 =1,从而可建立方程,由此可求椭圆C的离心率.
=1,从而可建立方程,由此可求椭圆C的离心率.
解答:解:由题意,∵直线y=x与椭圆 =1的交点在x轴上的射影恰好是椭圆的焦点
=1的交点在x轴上的射影恰好是椭圆的焦点
∴(c,c)满足椭圆 =1
=1
∴
∴a2c2+(a2-c2)c2=a2(a2-c2)
∴e4-3e2+1=0
∴
∵0<e<1
∴
故选A
点评:本题重点考查椭圆的几何性质,考查椭圆的标准方程,解题的关键是构建离心率方程,属于基础题.
 =1的交点在x轴上的射影恰好是椭圆的焦点,可得(c,c)满足椭圆
=1的交点在x轴上的射影恰好是椭圆的焦点,可得(c,c)满足椭圆 =1,从而可建立方程,由此可求椭圆C的离心率.
=1,从而可建立方程,由此可求椭圆C的离心率.解答:解:由题意,∵直线y=x与椭圆
 =1的交点在x轴上的射影恰好是椭圆的焦点
=1的交点在x轴上的射影恰好是椭圆的焦点∴(c,c)满足椭圆
 =1
=1∴

∴a2c2+(a2-c2)c2=a2(a2-c2)
∴e4-3e2+1=0
∴

∵0<e<1
∴

故选A
点评:本题重点考查椭圆的几何性质,考查椭圆的标准方程,解题的关键是构建离心率方程,属于基础题.

练习册系列答案
相关题目
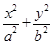 =1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为 B.
B. C.
C. D.
D.
 =1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为


