[题目]已知从地去地有①或②两条路可走.并且汽车走路①堵车的概率为.汽车走路②堵车的概率为.若现在有两辆汽车走路①.有一辆汽车走路②.且这三辆车是否堵车相互之间没有影响.(1)若这三辆汽车中恰有一辆汽车被堵的概率为.求走路②堵车的概率,的条件下.求这三辆汽车中被堵车辆的辆数的分布列和数学期望. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知从地去地有①或②两条路可走，并且汽车走路①堵车的概率为，汽车走路②堵车的概率为，若现在有两辆汽车走路①，有一辆汽车走路②，且这三辆车是否堵车相互之间没有影响，

（1）若这三辆汽车中恰有一辆汽车被堵的概率为，求走路②堵车的概率；

（2）在（1）的条件下，求这三辆汽车中被堵车辆的辆数的分布列和数学期望.

【答案】(1) ；(2)分布列见解析；.

【解析】

试题分析：

（1）根据独立事件同时发生的概率得到关于的方程，解得即为所求．（2）由题意的到随机变量的所有可能取值，并分别求出相应的概率，列成表格即可得到分布列，根据定义可得期望．

试题解析：

(1)由已知条件得，

即，

∴

即走路②堵车的概率为．

(2)由题意得的所有可能取值为

，

∴随机变量的分布列为

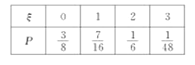
所以

练习册系列答案

(1)若x∈[－，]，且a∥(b＋c)，求x的值；

(2)若存在x∈R，使得(a＋d)⊥(b＋c)，求k的取值范围．

【题目】（本小题共分）

若或，则称为和的一个位排列，对于，将排列记为，将排列记为，依此类推，直至，对于排列和，它们对应位置数字相同的个数减去对应位置数字不同的数，叫做和的相关值，记作，例如，则，，若，则称为最佳排列．

（Ⅰ）写出所有的最佳排列．

（Ⅱ）证明：不存在最佳排列．

（Ⅲ）若某个（是正整数）为最佳排列，求排列中的个数．

【题目】已知曲线C1：，曲线C2：．

（1）指出C1，C2各是什么曲线，并说明C1与C2公共点的个数；

（2）若把C1，C2上各点的纵坐标都压缩为原来的一半，分别得到曲线，．写出，的参数方程．与公共点的个数和C1与C2公共点的个数是否相同？说明你的理由．

【题目】写出下列各组命题构成的“或”、“且”以及“非”形式的命题，并判断它们的真假．

(1)：是有理数，：是整数；

(2)：不等式的解集是，：不等式的解集是．

【题目】已知

（1）求函数在的极值.

（2）证明：在有且仅有一个零点.

【题目】 (1)已知正数a，b满足a＋b＝1，求证：a2＋b2≥；

(2)设a、b、c为△ABC的三条边，求证：a2＋b2＋c2<2(ab＋bc＋ca)．

【题目】某企业生产、两种产品，生产每产品所需的劳动力和煤、电消耗如下表：

产品品种	劳动力（个）	煤	电

已知生产产品的利润是万元，生产产品的利润是万元.现因条件限制，企业仅有劳动力个，煤，并且供电局只能供电，则企业生产、两种产品各多少吨，才能获得最大利润？

【题目】某公司今年年初用25万元引进一种新的设备，投入设备后每年收益为21万元．该公司第年需要付出设备的维修和工人工资等费用的信息如下图．

（1）求；

试题分类