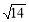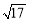题目内容
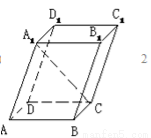
如图,四边形ABCD为矩形,AD  平面ABE,AE=EB=BC=2,F为CE上的点.且BF
平面ABE,AE=EB=BC=2,F为CE上的点.且BF  平面ACE.
平面ACE.

(1)求证:平面ADE 平面BCE;
平面BCE;
(2)求四棱锥E-ABCD的体积;
(3)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN 平面DAE.
平面DAE.
(1)略; (2) 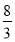 ;(3)N为线段CE上靠近C点的一个三等分点.
;(3)N为线段CE上靠近C点的一个三等分点.
【解析】
试题分析:(1)由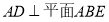 且
且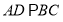 可得
可得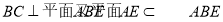 ,所以有
,所以有
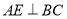 ,同理可得
,同理可得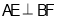 ,
,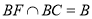
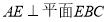 ,所以
,所以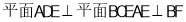 .
.
(2)四棱锥的体积 ,
,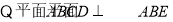
 四棱锥的高即点E到AB的距离,所以
四棱锥的高即点E到AB的距离,所以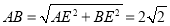 ,四棱锥E-ABCD的体积为
,四棱锥E-ABCD的体积为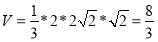 .
.
(3)在三角形ABC过M点作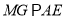 交
交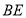 于
于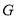 点,在三角形BEC中过G点作
点,在三角形BEC中过G点作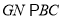 交EC与N点,连MN,则由比例关系易得
交EC与N点,连MN,则由比例关系易得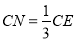 ,
,
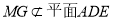
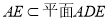
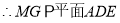 同理,
同理,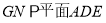
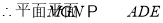 又
又
 N为线段CE上靠近C点的一个三等分点.
N为线段CE上靠近C点的一个三等分点.
试题解析:(1) 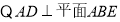 且
且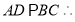
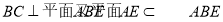

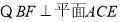
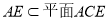
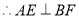 又
又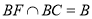
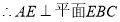
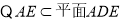
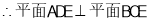 .
.
(2)因为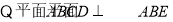
 四棱锥的高即点E到AB的距离,
四棱锥的高即点E到AB的距离,
在直角三角形中ABE中, ,所以,
,所以,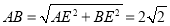 .四棱锥E-ABCD的体积为
.四棱锥E-ABCD的体积为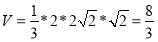 .
.
(3)在三角形ABC过M点作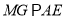 交
交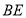 于
于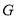 点,在三角形BEC中过G点作
点,在三角形BEC中过G点作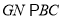 交EC与N点,连MN,则由比例关系易得
交EC与N点,连MN,则由比例关系易得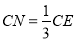 ,
,
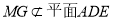
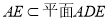
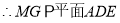 同理,
同理,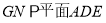
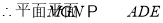 又
又
 N为线段CE上靠近C点的一个三等分点.
N为线段CE上靠近C点的一个三等分点.
考点:空间立体几何的证明与运算.

练习册系列答案
相关题目