题目内容
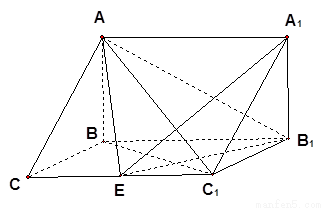
如图,在三棱拄![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]()
![]()
![]()
(1)求证:![]() ;
;![]()
(2)试在棱![]() (不包含端点
(不包含端点![]() 上确定一点
上确定一点![]() 的位置,
的位置,![]()
使得![]() ;
;![]()
(3) 在(2)的条件下,求二面角![]() 的平面角的正切值.
的平面角的正切值.![]()
![]() 为
为![]() 的中点时,
的中点时,![]()
![]() ,
,
解析:
证(Ⅰ)因为![]() 侧面
侧面![]() ,故
,故![]()
![]()
在![]() 中,
中,![]() 由余弦定理有
由余弦定理有 ![]()
![]()
![]()
 故有
故有 ![]()
![]()
而 ![]() 且
且![]() 平面
平面![]()
![]()
![]()
![]()
![]()
![]()
(Ⅱ)由![]()
![]()
从而![]() 且
且![]() 故
故![]()
![]()
不妨设 ![]() ,则
,则![]() ,则
,则![]()
![]()
又![]() 则
则![]()
![]()
在![]() 中有
中有 ![]() 从而
从而![]() (舍负)
(舍负)![]()
故![]() 为
为![]() 的中点时,
的中点时,![]()
![]()
 法二:以
法二:以![]() 为原点
为原点![]() 为
为![]() 轴,设
轴,设![]() ,则
,则![]() 由
由![]() 得
得 ![]() 即
即![]()

![]()
化简整理得 ![]() ,
,![]() 或
或 ![]()
![]()
当![]() 时
时![]() 与
与![]() 重合不满足题意
重合不满足题意![]()
当![]() 时
时![]() 为
为![]() 的中点
的中点![]()
故![]() 为
为![]() 的中点使
的中点使![]()
![]()
(Ⅲ)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]()
![]()
连![]() 则
则![]() ,连
,连![]() 则
则![]() ,连
,连![]() 则
则![]()
![]()
连![]() 则
则![]() ,且
,且![]() 为矩形,
为矩形,![]()
![]()
 又
又![]() 故
故![]() 为所求二面角的平面角
为所求二面角的平面角![]()
在![]() 中,
中,![]()
![]()

法二:由已知![]() , 所以二面角
, 所以二面角![]() 的平面角
的平面角![]() 的大小为向量
的大小为向量![]() 与
与![]() 的夹角
的夹角
因为![]()
![]()
故 

练习册系列答案
相关题目

 中,
中, 侧面
侧面 ,已知
,已知


 ;(4分)
;(4分) 为
为 的中点时,求二面角
的中点时,求二面角 的平面角的正切值.(8分)
的平面角的正切值.(8分) 中,
中, 侧面
侧面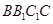 ,
,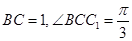

 (不包含端点
(不包含端点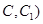 上确定一点
上确定一点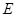 的位置,使得
的位置,使得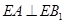 ;
;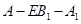 的平面角的正切值.
的平面角的正切值.
 中,
中,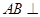 侧面
侧面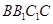 ,
,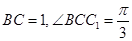

 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得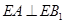 ;
;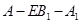 的平面角的正切值.
的平面角的正切值.